Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 102
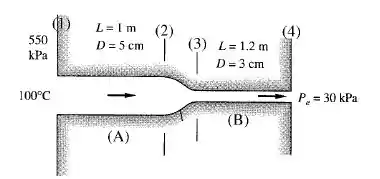
Ar a 550 kPa e 100°C entra em um tubo liso de 1 m de comprimento e em seguida passa por um segundo tubo liso para um reservatório a 30 kPa, como na figura abaixo. Utilizando o diagrama de Moody para determinar , calcule a vazão em massa por esse sistema. O escoamento está bloqueado?
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)
Antes de sairmos fazendo conta, vamos pensar e discutir um pouco sobre essa questão, beleza?
Você vai concordar comigo que e
As seções mais relevantes no nosso problema são a 1, 2, 3 e 4. Temos também que , ou seja, esse tubo pequeno COM CERTEZA será bloqueado com uma pressão muito maio do que 30 kPa.
Uma das formas seria chutar o valor de e trabalhar de modo a obter . Tomando um valor constante de viscosidade médio . Assumindo expansão isentrópica da seção 1, partindo do reservatório, escoamento com atrito através do tubo na seção A, e também expansão isentrópica da seção 2 para 3 e um segundo coeficiente de atrito para seção 4, ou seja, para o tubo B.
Passo 2
Vou te dar essa colher de chá e te dar já qual é o valor de que causaria um , esse valor é de 0,18.
O que nos dará um valor de , fazendo com que no diagrama de Moody se obtenha um valor de
A tabela B.3:
Passo 3
O tubo A é tão pequeno que Ma muda bem pouco!!!! Em lemos que . Agora, em , determina-se que . Portanto, o que nos dará um e .
Parando no cálculo de , e , do diagrama de Moody tiramos que .
Esse último valor deveria ser exatamente igual a se o número de Mach na saída for 1. Ok, nosso valor não está zero mas estamos bem próximos.
Portanto, o valor da vazão mássica das condições obtidas na seção 1 é: