O escoamento compressível em um duto com adição de calor, seção 9.8, supõe quantidade de movimento e vazão em massa constantes, porém entalpia de estagnação variável. Tal escoamento normalmente se denomina escoamento de Rayleigh, e uma linha representativa de todas as possíveis variações das propriedades em um diagrama temperatura-entropia denomina-se linha de Rayleigh. Admitindo o ar escoando na condição de , , e , desenhe uma curva de Rayleigh do escoamento para uma faixa de velocidades desde muito baixas (Ma > 1). Comente a respeito do significado do ponto de entropia máxima sobre essa curva.

Agora é pensarmos quais são as equações algébricas que regem nosso problema!!! Equação da quantidade de movimento (momentum), continuidade e entropia.

Para entropia, lembre-se que:

Vamos simplesmente variar a velocidade V de 10 m/s até 800 m/s por exemplo. Depois calcular a densidade, pressão na equação de momentum e temperatura e a entropia da terceria equação que escrevemos. Depois vamos plotar temperatura vs entropia.

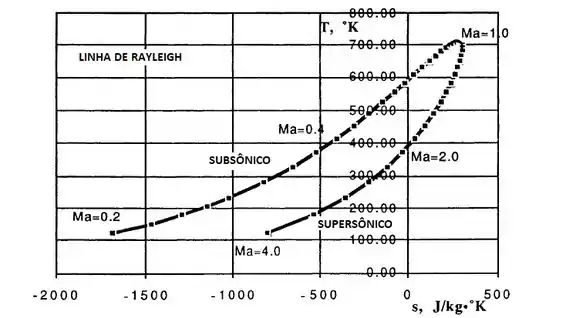
Esse resultado vai formar o que chamamos de linha de Rayleigh como é mostrado abaixo. Alguns números de Mach são listados, subsônico no topo, supersônico na parte mais abaixo e sônico exatamente na região de maior entropia, ou seja, quando .