Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 59

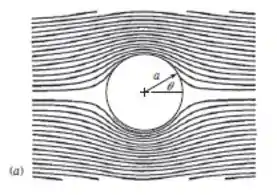
59 – Considere o escoamento não viscoso em torno de um cilindro com circulação nula, como na Fig. 8.14a (mostrada abaixo). Encontre (a) o ponto sobre a superfície frontal onde a aceleração do fluido amáx é máxima e (b) a intensidade de amáx. (c) Se a velocidade da corrente é 1 m/s, encontre o diâmetro do cilindro para o qual amax é 10 vezes a aceleração da gravidade. Comente.

Passo 1

Vamos relembrar que a aceleração é definida como a taxa de variação de da velocidade com o tempo. Com isso, a aceleração vai ser a seguinte:

a = d u d t

Onde, podemos escrever a derivada da velocidade com o tempo também da seguinte forma:

d u d t = u ∞ d d u d θ

Assim,

a = u ∞ d d u d θ

Passo 2

Como neste exercício temos um escoamento sobre um cilindro circular, assim a velocidade u é dada por:

u = 2 u ∞ s e n ( θ )

Onde, u ∞ , é a velocidade da corrente fluida.

Vamos ter que para a aceleração máxima:

a = u ∞ d d d θ 2 u ∞ s e n θ

a = 2 u ∞ 2 d d d θ s e n θ

Resolvendo a derivada:

d d θ s e n θ = c o s ⁡ ( θ )

Assim,

a = 2 u ∞ 2 d c o s ⁡ ( θ )

Passo 3

Para acharmos agora o ponto de θ onde a aceleração é máxima, basta você derivar a equação da aceleração encontrada e igualar a zero

d a d θ = d d θ 2 u ∞ 2 d cos ⁡ θ = 0

d d θ 2 u ∞ 2 d cos ⁡ θ = 2 u ∞ 2 a s e n ( θ )

2 u ∞ 2 d s e n θ = 0

Ou seja,

s e n θ = 0

θ = s e n - 1 0

Os valores possíveis para θ são:

θ = 0 ° ; θ = 180 °

Passo 4

Vamos agora encontrar o diâmetro pelo qual a aceleração máxima é 10 vezes a gravidade

a m á x = 10 g

a m á x = 10 9,81 m s 2 = 98,1 m s 2

Sendo que a aceleração máxima ocorre quando θ = 0, assim

a m á x = 2 u ∞ 2 d cos ⁡ 0 = 2 u ∞ 2 d

Isolando o diâmetro d,

d = 2 u ∞ 2 a m á x

Aplicando os valores:

d = 2 1 m s 2 98,1 m s 2

d = 0,0 2   m = 20   m m

Resposta

θ = 0 ° ; θ = 180 °

d = 0,02   m = 20   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma função corrente incompressível é definida por ψ x , y = U L 2 ( 3 x 2 y - y 3 ) em que UeL são constantes (positivas). Em que parte deste capítulo há um gráfico das linhas de corrente desse escoam
Investigue o potencial de velocidade ϕ = K x y ,K = c o n s t a n t e . Faça um esboço de linhas equipotenciais no plano xy completo, encontre quaisquer pontos de estagnação e faça um esboço aproximad
O Problema P4.38 pede para você encontrar a distribuição de pressão p ( r ) para a rotação de corpo sólido de um fluído, v θ = C r . Se z é “para cima, o resultado pode ser escrito da seguinte maneira
Investigue a função corrente ψ = K x 2 - y 2 ,K = c o n s t a n t e . Trace o gráfico de algumas linhas de corrente no plano xy completo, determine quaisquer pontos de estagnação e interprete o que o
Um fluido sem atrito, incompressível, bidimensional é guiado, por duas paredes dispostas em forma de cunha, para uma pequena abertura na origem, como mostra a Figura P4.52. A largura na direção perpen