Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 9.Problemas - Ex. 71

Uma janela de vidro duplo, vertical, que tem 1   m de lado e um espaço de 25   m m preenchido com ar atmosférico, separa o ar quiescente de uma sala a T ∞ , i = 20 ° C do ar ambiente externo, também quiescente, a T ∞ , e = 22 0 ° C . As trocas radiantes entre as lâminas de vidro, assim como entre as lâminas de vidro e os seus ambientes adjacentes, podem ser desprezadas.

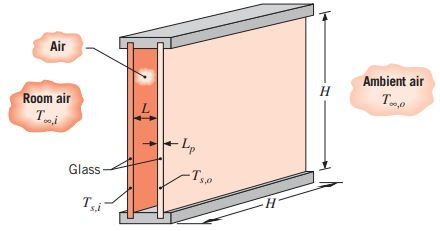
(a) Desprezando a resistência térmica associada à transferência de calor por condução através de cada lâmina de vidro, determine a temperatura correspondente de cada lâmina e a taxa de transferência de calor através da janela.

(b) Comente sobre a validade de se desprezar a resistência condutiva nas lâminas de vidro, se cada uma tiver uma espessura de L v = 6   m m .

Passo 1

Opa, beleza?

Vem comigo que juntos a gente resolve essa questão!

Letra a)

Começamos o nosso problema considerando que ocorrerá apenas convecção natural em nosso sistema, além disso, não ocorrem perdas de calor entre a passagem de energia da janela para os ambientes e vice-versa. Então:

q = h - i A T s , 1 - T ∞ , i = h - j A T s , 2 - T s , 1 = h - e A T ∞ , e - T s , 2

h - i T s , 1 - T ∞ , i = h - j T s , 2 - T s , 1 = h - e T ∞ , e - T s , 2

Assim, devemos obter os coeficientes convectivos associados as transferências de calor e verificar se atendem a condição imposta acima.

Para isso, vamos fazer um “chute” para as temperaturas de superfície:

T s , 1 = 69 ° C

T s , 2 = 162 ° C

Agora, vamos aos cálculos!

Passo 2

Analisando a primeira parte da nossa relação, ou seja, o ambiente interno, temos:

T - m = T s , 1   + T ∞ , 1 2

T - m = 69 + 20 2 = 44,5 ° C   ( 317,5   K )

Pela Tabela A.4, para o ar sob essa temperatura, obtemos:

ρ i n t = 1,1032   k g / m 3

c p i n t = 1007,7   J / k g ⋅ K

v i n t = 17,65 × 10 - 6   m 2 / s

k i n t = 27,6 × 10 - 3   W / m ⋅ K

P r i n t = 0,705

Calculando o número de Rayleigh:

R a H = g β ∆ T H 3 k ρ c p v

Substituindo os dados:

R a H = 9,8 ⋅ 1 317,5 ⋅ 69 - 20 ⋅ 1 3 27,6 × 10 - 3 1,1032 ⋅ 1007,7 ⋅ 17,65 × 10 - 6

R a H = 3,455 × 10 9

Calculando o coeficiente convectivo pela relação do número de Nusselt:

N u H = h - i H k = 0,825 + 0,387 R a H 1 6 1 + 0,492 P r 8 27 2

h - i = k H 0,825 + 0,387 R a H 1 6 1 + 0,492 P r 8 27

Substituindo os dados:

h - i = 27,6 × 10 - 3 1 ⋅ 0,825 + 0,387 ⋅ 3,455 × 10 9 1 6 1 + 0,492 0,705 8 27

h - i = 4,98   W / m 2 ⋅ K

Calculando o nosso fluxo de convecção:

q ' ' = h - i T s , 1 - T ∞ , i

q ' ' = 4,98 ⋅ 69 - 20

q ' ' = 244   W / m 2

Agora, devemos calcular os demais fluxos e compará-los!

Passo 3

Para a segunda parte da nossa relação, devemos calcular o coeficiente convectivo externo e o seu fluxo de calor:

T - m = T ∞ , e + T s , 2 2

T - m = 220 + 162 2 = 191 ° C   ( 464   K )

Pela Tabela A.4, para o ar sob essa temperatura, obtemos:

ρ e x t = 0,7523   k g / m 3

c p e x t = 1023,5   J / k g ⋅ K

v e x t = 34,95 × 10 - 6   m 2 / s

k e x t = 38,3 × 10 - 3   W / m ⋅ K

P r e x t = 0,685

Calculando o número de Rayleigh:

R a L = g β ∆ T L 3 k ρ c p v

Substituindo os dados:

R a L = 9,8 ⋅ 1 388,5 ⋅ 162 - 69 ⋅ 25 × 10 - 3 3 3 2,9 × 10 - 3 0 , 8996 ⋅ 10 12,9 ⋅ 25,15 × 10 - 6

R a H = 40404,6

Calculando o coeficiente convectivo pela relação do número de Nusselt:

N u H = h - j H k = 0,42 R a L 1 4 P r 0,012 H L - 0,3

h - j = k H 0,42 R a L 1 4 P r 0,012 H L - 0,3

Substituindo os dados:

h - j = 32,9 × 10 - 3 1 ⋅ 0,42 ⋅ 40404,6 1 4 ⋅ 0,692 0,012 ⋅ 1 25 × 10 - 3 - 0,3

h - j = 2,58   W / m 2 ⋅ K

Calculando o nosso fluxo de convecção:

q ' ' = h - j T ∞ , e - T s , 2

q ' ' = 4,205 ⋅ 220 - 162

q ' ' = 243,9   W / m 2

Percebemos que temos uma proximidade com o valor encontrado anteriormente para o ambiente interno.

Agora, devemos conferir a última parte da nossa equação!

Passo 4

Para a última parte da nossa relação, devemos calcular o coeficiente convectivo da nossa junta e o seu fluxo de calor:

T - m = T s , 2 + T s , 1 2

T - m = 1 62 + 69 2 = 11 5,5 ° C   ( 388,5   K )

Pela Tabela A.4, para o ar sob essa temperatura, obtemos:

ρ j u n = 0,7523   k g / m 3

c p j u n = 1023,5   J / k g ⋅ K

v j u n = 34,95 × 10 - 6   m 2 / s

k j u n = 38,3 × 10 - 3   W / m ⋅ K

P r j u n = 0,685

Calculando o número de Rayleigh:

R a H = g β ∆ T H 3 k ρ c p v

Substituindo os dados:

R a H = 9,8 ⋅ 1 464 ⋅ 220 - 162 ⋅ 1 3 38,3 × 10 - 3 0,7523 ⋅ 1023,5 ⋅ 34,95 × 10 - 6

R a H = 7,054 × 10 8

Calculando o coeficiente convectivo pela relação do número de Nusselt:

N u H = h - e H k = 0,825 + 0,387 R a H 1 6 1 + 0,492 P r 8 27 2

h - e = k H 0,825 + 0,387 R a H 1 6 1 + 0,492 P r 8 27

Substituindo os dados:

h - e = 38,3 × 10 - 3 1 ⋅ 0,825 + 0,387 ⋅ 7,054 × 10 8 1 6 1 + 0,492 0,685 8 27

h - i = 4,205   W / m 2 ⋅ K

Calculando o nosso fluxo de convecção:

q ' ' = h - i T s , 2 - T s , 1

q ' ' = 2,58 ⋅ 162 - 69

q ' ' = 2 40   W / m 2

Percebemos apenas um ligeiro desvio entre os fluxos térmicos encontrados para as três partes da nossa equação, assim podemos assumir as temperaturas superficiais das placas adotadas como valores bem próximos dos reais.

T s , 1 = 69 ° C

T s , 2 = 162 ° C

Passo 5

Letra b)

Aqui, devemos verificar se a resistência condutiva poderia ser desprezada, e para isso devemos calcular as resistências convectivas com os coeficientes convectivos encontrados na letra (a), utilizaremos a seguinte equação:

R c o n v = 1 h A

Resistência interna:

R c o n v ,   i n t = 1 h - i A = 1 h - i H 2

R c o n v ,   i n t = 1 4,98 ⋅ 1 2 = 0,20   m 2 ⋅ K / W

Resistência externa:

R c o n v ,   e x t = 1 h - e A = 1 h - e H 2

R c o n v ,   e x t = 1 4,205 ⋅ 1 2 = 0,2 4   m 2 ⋅ K / W

Resistência da junta:

R c o n v ,   j u n = 1 h - j A = 1 h - j H 2

R c o n v ,   j u n = 1 2,58 ⋅ 1 2 = 0 , 39   m 2 ⋅ K / W

Agora que temos uma ideia das resistências convectivas associadas ao nosso sistema, devemos calcular a condutiva.

Pela Tabela A.3, para o vidro, obtemos:

k v i d r o = 1,4   W / m ⋅ K

Então, temos que a resistência condutiva do nosso sistema é:

R c o n d = L k A = 2 L k H 2

R c o n d = 2 ⋅ 6 × 10 - 3 1,4 ⋅ 1 2 = 0,009   m 2 ⋅ K / W

Como a nossa resistência condutiva possuí um valor muito pequeno comparado aos outros, podermos desprezá-la!

Até a próxima questão!

Resposta

T s , 1 = 69 ° C

T s , 2 = 162 ° C

R e s i s t ê n c i a   C o n d u t i v a   D e s p r e z í v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

63 - Considere um pino (aleta) horizontal com 6m m de diâmetro e 60m m de comprimento fabricado em aço-carbono não ligado ( k = 57W / ( m · K ) ,ε = 0,5 ) . A base do pino é mantida a 150℃ ℃, enquanto
58 - Uma tubulação horizontal, com 12,5m m de diâmetro e uma temperatura superficial externa de 240℃ ℃, está localizada no interior de uma sala cujo ar se encontra a uma temperatura de 20℃ ℃. Estime a
64 - Considere o tubo de água quente do Problema 7.56, mas sob condições nas quais o ar ambiente não está em escoamento cruzado sobre o tubo, estando sim quiescente. Levando em conta os efeitos da rad
60 - Um cabo elétrico horizontal com 25m m de diâmetro tem uma taxa de dissipação térmica de 30W / m . Se a temperatura do ar ambiente é de 27℃ ℃, estime a temperatura superficial do cabo.
62 - A temperatura superficial máxima no eixo, com 20m m de diâmetro, de um motor que opera no ar ambiente a 27℃ ℃, não deve exceder 87 ℃ ℃. Devido à dissipação de potência no interior da carcaça do m