Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 7.Problemas - Ex. 70
7.70
Em algumas faixas de velocidade, vórtices são formados atrás de cilindros rombudos colocados atravessados em um escoamento. Os vórtices, alternadamente, partem do topo e do fundo do cilindro, como mostrado, causando uma força alternante normal à velocidade da corrente livre. Supõese que a frequência de formação dos vórtices, f, depende de ρ, d, V e μ. Use análise dimensional para desenvolver uma relação funcional para f. Esteiras de vórtices ocorrem no arpadrão sobre dois cilindros com razão de diâmetros igual a 2. Determine a razão entre as velocidades para haver semelhança dinâmica e a razão entre as frequências de formação dos vórtices.
Passo 1
Primeiramente, vamos fazer uma analise dimensional e aplicar o teorema de pi de Buckingham.
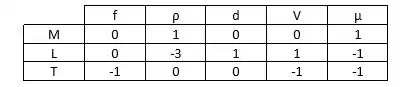
Passo 2
Escolhendo ρ,V e D como parâmetros para determinar os adimensionais:
Colocado as unidades em evidência:
M: a=0
L: -3a+b+c =0
T: -1 – b=0
Passo 3
Colocado as unidades em evidência:
M: 1+a=0
L: -1-3.a+b+c =0
T: -1 – b=0
Sendo assim, a relação da função será:
Passo 4
Para ter uma similaridade dinâmica entre os escoamentos, é necessário que haja uma igualdade entre o caso 1 e o caso 2:
Passo 5
Igualmente para o outro adimensional: