Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 87
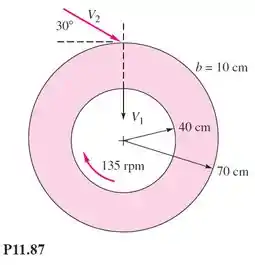
87 – A Figura P11.87 mostra uma turbina radial idealizada. O escoamento absoluto entra a 30° e sai radialmente no seu interior. A vazão é de 3,5 m3/s de água a 20 °C. A pá tem largura constante de 10 cm. Calcule a potência teórica desenvolvida.
Passo 1
Neste exercício foi te pedido a potência teórica desta turbina radial idealizada, ou seja, te pediu para determinar a potência de eixo gerada por uma turbina ideal. Quando se fala em uma turbomáquina ideal sempre podemos pensar nas equações de Euler das turbomáquina para fazermos os cálculos, que são equações baseadas na idealidade de uma turbomáquina.
Vamos então usar as equações de Euler.
Passo 2
Relembrando das equações de Euler das turbomáquinas, que a equação de potência para uma turbomáquina ideal é a seguinte
Onde,
-P é a potência de eixo desenvolvida pela turbina, neste caso;
-ρ é a densidade da água, 1000 kg/m3;
-Q é a vazão;
-u2 é a velocidade periférica na entrada;
-u1 é a velocidade periférica na saída;
-Vt2 é a velocidade circunferencial (tangencial) na entrada (2);
-Vt1 é a velocidade circunferencial (tangencial) na saída (1);
Vamos a seguir saber como determinar as velocidades
Passo 3
A velocidade periférica, u, é calculada pela seguinte expressão
Onde,
-r é o raio do rotor (externo, r2=1,2m, e interno, r1=0,8m);
-ω é a velocidade angular;
A velocidade angular, lembrando, é expresso em termos da rotação, n, da seguinte forma
Então, a expressão da velocidade periférica agora é
Aplicando essa expressão na entrada, 2, e na saída do rotor
Onde,
-u2 é a velocidade periférica na entrada;
-u1 é a velocidade periférica na saída;
-r2 é o raio externo do rotor, r2=0,7m;
-r1 é o raio interno do rotor, r1=0,4 m;
-n é a rotação em rpm.
Calculando as velocidades periféricas
Passo 4
Para expressarmos as velocidades circunferenciais (tangenciais), Vt, vamos ter que avaliar a posição de entrada e de saída do fluido pela figura 11.87.
A velocidade circunferencial (ou tangencial) na entrada, V2, se relaciona matematicamente com a velocidade radial da entrada, W2, com a seguinte expressão
Onde,
-W2 é a velocidade radial na entrada;
-Vt2 é a velocidade circunferencial na entrada;
-α é o ângulo referente a velocidade circunferencial na entrada do rotor, ângulo de V2, α=30º;
Isolando Vt2,
Lembrando que 1/tan(α) é igual a cot(α), assim
Para Vt1, que é a velocidade circunferencial na saída do rotor, podemos determina-lo pela seguinte equação
Onde,
-W1 é a velocidade radial na saída;
-Vt1 é a velocidade circunferencial na saída;
-θ é o ângulo referente a velocidade radial W1, θ=90º.
Passo 5
Vamos expressar matematicamente as velocidades radias
Velocidade radial na entrada
Onde,
-W2 é a velocidade radial da água na entrada;
-Q é a vazão;
-A2 é a área da pá referente a entrada;
A área da pá é definida como
Onde,
-r2 é o raio externo do rotor, r2=0,8m;
-b2 é a largura da pá.
Como foi dito que a largura da pá é constante, então
Substituindo,
Analogamente,
Onde,
-r1 é o raio interno do rotor, r1=0,4 m;
-b é a largura da pá.
Passo 6
Definimos as expressões das velocidades radias. Vamos calcula-las
Para a velocidade radial da entrada, W2
Para a velocidade radial da saída, W1
Passo 7
Calculando as velocidades circunferenciais
-Vt2
Aplicando os valores
-Vt1
Aplicando os valores
Passo 8
Voltando na expressão da potência teórica
Agora é só aplicar os valores