Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 103
103 – Uma enorme TEEV Darrieus foi construída pelo U. S. Department of Energy próximo de Sandia, Novo México. Ela tem 18,3 m de altura e 9,1 m de diâmetro, com uma área de varredura de 111,5 m2. Se a turbina for mantida em uma rotação de 90 rpm, use a Figura 11.32 para traçar a potência de eixo prevista em kW em função da velocidade do vento no intervalo de V=8 até 64 km/h.
Passo 1
Neste exercício teremos que plotar um gráfico de PTE vs Vv (potência da turbina eólica vs velocidade do vento). Para isso precisaremos de uma expressão que relaciona PTE em função de Vv.
Passo 2
Determinando uma relação entre potência da TEEV e velocidade do vento:
Pela figura, temos a relação da razão das velocidades, , e o coeficiente de potência, CP, que é função dessa razão de velocidades
Onde,
-ω é a rotação do rotor da turbina eólica, Rad/s;
-r é o raio da hélice da turbina (r=DTE/2);
-Vv é a velocidade do vento.
A expressão do coeficiente de potência para uma turbina eólica é
Onde,
-PTE é a potência gerada pela turbina eólica;
-ρar é a densidade do ar, ρar= 1,20kg/m3;
-A é a área da hélice;
-Vv é a velocidade do vento;
Isolando PTE:
Passo 3
A área A é função do diâmetro da turbina:
Substituindo:
Passo 4
Vamos precisar determinar uma função de Cp em função da velocidade Vv. Você pode fazer isso usando os dados da figura 11.32 e com o auxílio de uma ferramenta gráfica, com o plote dos dados de Cp vs razão de velocidades (ωr/Vv), você consegue obter uma expressão de Cp em função de Vv
A rotação precisa ser convertida para Rad/s. Convertendo rpm (Rev/m) para Rad/s:
Eu usei o EXCEL para realizar tal tarefa, pegando os seguintes dados da razão de velocidades e os valores de Cp correspondentes:
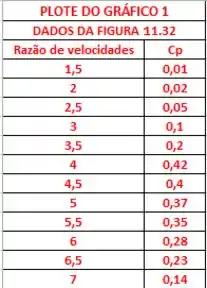
Passo 5
Com os dados anteriores, fiz o plote e obtive o seguinte gráfico:
Gráfico 1 – Cp vs Razão de velocidades. Onde, a curva preta pontilhada é a linha de tendência representada pela equação na parte de cima do gráfico, e a curva em azul é a referente aos dados da tabela.
Pelo gráfico 1, você pode ver que a eq. que representa a curva de Cp vs Razão de velocidades é a seguinte:
Na qual,
Assim,
Com os valores de ω e r já conhecidos,
Então, podemos expressar Cp apenas em função de VV:
Passo 6
Pegando a Eq1 e calculando o que já se conhece:
Colocando a Eq2 no lugar de Cp teremos uma equação de PTE apenas em função de Vv.
Passo 7
Com a Eq3 e com a Eq2 podemos plotar um gráfico de P vs Vv, atribuindo valores para Vv e calculando o valor de P correspondente.
Utilizando o EXCEL, os seguintes dados foram obtidos para a potência na faixa de Vv de 8 a 64 km/h:
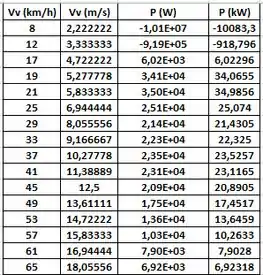
Com os dados acima obteve-se o seguinte gráfico:
Gráfico 2 – P vs VV.
Portanto, este é o gráfico que foi solicitado no problema.
Resposta
