Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 64

A absortividade espectral α λ e a refletividade espectral ρ λ de um material difuso espectralmente seletivo são mostradas a seguir.

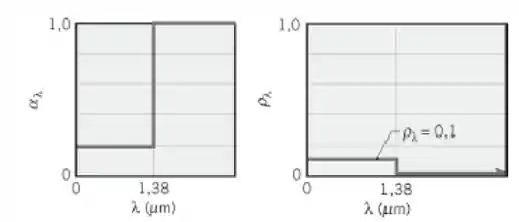
(a) Esboce a transmissividade espectral τ λ .

(b) Se irradiação solar com G S   = 750   W / m 2 e distribuição espectral de um corpo negro a 5800   K incide sobre esse material, determine as frações da irradiação que é transmitida, que é refletida e que é absorvida pelo material.

(c) Se a temperatura desse material é de 350   K , determine a emissividade ε .

(d) Determine o fluxo térmico radiante líquido para o material.

Passo 1

Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)

I - D i f u s ã o   e s p e c t r a l   é   p r o p r o c i o n a l   a   E λ ,   b λ , 5800   K

I I - S u p e r f i c i e   é   d i f u s a

Passo 2

(a)

Agora temos que do balanço de energia, de acordo com a equação 12.54 temos:

ρ λ + α λ + τ λ = 1

Ou seja:

τ λ = 1 - ρ λ + α λ

Com isso vamos montar o gráfico para nossa difusividade espectral.

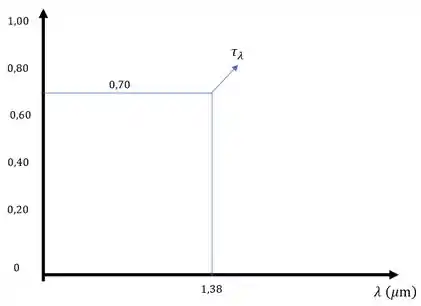
Passo 3

(b)

Da equação 12.61 temos que a transmissividade devido a radiação solar é dada por:

τ s = ∫ 0 ∞ τ λ G λ ,   s d λ ∫ 0 ∞ G λ ,   s d λ = ∫ 0 ∞ τ λ E λ ,   b λ , 5800   K d λ E b 5800   K

Onde λ 1 T s = 1,38 ⋅ 5800 = 8000 μ m ⋅ K e da tabela 12.1   F 0 → λ 1

τ s = τ λ F 0 → λ 1 = 0,7 ⋅ 0,856 = 0,599

Das equações 12.58 e 12.63 :

ρ s = ∫ 0 ∞ τ λ G λ ,   s d λ G s = τ λ ,   1 ⋅ F 0 → λ 1

ρ s = 0,086

Por fim temos:

α S = 1 - ρ S + τ S

α S = 0,315

Passo 4

(c)

Para a superfície a emissividade pode ser determinada da equação 12.43 , como a superfície é difusa de acordo com a equação 12.67 com α λ = ε λ , temos:

ε λ = ∫ 0 ∞ α λ E λ ,   b T s d λ E λ ,   b T s = α λ ,   1 ⋅ F 0 → 1,38   μ m + α λ ,   2 ⋅ 1 - F 0 → 1,38   μ m

Onde λ 1 T s = 1,38 ⋅ 350 = 483 μ m ⋅ K e da tabela 12.1   F 0 → λ 1

τ s = τ λ F 0 → λ 1 ≈ 0

ε λ = α λ ,   2 = 1

Passo 5

(d)

Fazendo o balanço de radiatividade podemos encontrar fluxo térmico radiante.

q r a d ' ' = G s - ρ s G s - τ s G s - E = α s G s - E

q r a d ' ' = 0,315 ⋅ 750   W m 2 - 5,67 ⋅ 10 - 8 W m 2 ⋅ K 4 ⋅ 350   K 4

q r a d ' ' = -   615 W m 2  

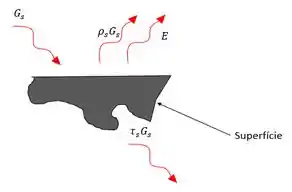
Isso é tudo pessoal! \o/

Resposta

(a) Gráfico vide passo a passo, τ λ = 1 - ρ λ + α λ .

(b)   α S = 0,315

(c) ε λ = α λ ,   2 = 1

(d) q r a d ' ' = -   615 W m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A refletividade do alumínio revestido com sulfato de chumbo é 0,35 para uma radiação com comprimentos de onda inferiores a 3 μ m e 0,95 para uma radiação superior a 3 μ m. Determine a refletividade mé
As variações da emissividade espectral de duas superfícies são indicadas na figura a seguir. Determine a emissividade média de cada superfície a T =3.000 K. Além disso, determine a absortividade e a r
A variação da transmissividade espectral de uma janela de vidro de 0,6 cm de espessura é indicada na figura a seguir. Determine a transmissividade média dessa janela para a radiação solar ( T ≈ 5.800
O que é um corpo cinza? Como ele difere de um corpo negro? O que é superfície cinza difusa?
Defina as propriedades emissividade e absortividade. Quando essas duas propriedades são iguais?