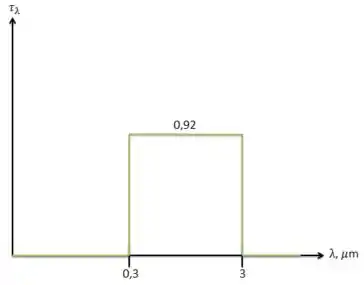
A variação da transmissividade espectral de uma janela de vidro de 0,6 cm de espessura é indicada na figura a seguir. Determine a transmissividade média dessa janela para a radiação solar ( 5.800 K) e a radiação proveniente de superfícies na temperatura ambiente ( 300 K). Além disso, determine a quantidade de radiação solar transmitida através da janela para uma radiação solar incidente de 650 W/m2.

A transmissividade média é calculada por:

Usando as informações do perfil:

Podemos aproximar utilizando a função de radiação do corpo negro :

Vamos usar isso para encontrar a emissividade hemisférica total:

Vamos calcular primeiro para a temperatura de 5.800 K. Pela tabela 12-2 do capítulo 12 do livro temos que para:

Então, nossa transmissividade a 5.800 K é:

Podemos aproximar utilizando a função de radiação do corpo negro :

Vamos usar isso para encontrar a emissividade hemisférica total:

Vamos calcular primeiro para a temperatura de 5.800 K. Pela tabela 12-2 do capítulo 12 do livro temos que para:

Então, nossa transmissividade a 5.800 K é:

Agora iremos determinar a transmissividade a 300 K. Pela tabela 12-2 do capítulo 12 do livro temos que para:

Então, nossa transmissividade a 300 K é:

Por fim, vamos determinar a irradiação que é transmitida pela janela. A radiação transmitida é dada por:

Como a radiação vem do Sol, iremos usar a transmissividade em 5.800 K. A radiação transmitida é: