Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 65

Considere um grande forno com paredes opacas, difusas e cinzas, que se encontram a 3000   K e cuja emissividade é de 0,85 . Um pequeno objeto difuso e espectralmente seletivo é mantido no interior do forno a uma temperatura de 300   K .

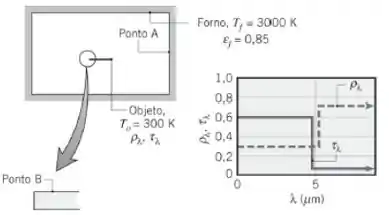
Para os pontos especificados sobre a parede do forno ( A ) e sobre o objeto ( B ) , indique os valores de ε ,   α ,   E ,   G   e J .

Passo 1

Vamos lá!! antes de mais nada precisamos fazer nossas famosas considerações. Hehe (u.u)

I - A s   p a r e d e s   d o   f o r n o   s ã o   i s o t e r m i c a s ,   d i f u s a s   e   u m   c o p o   c i n z a

I I - S u p e r f i c i e   é   d i f u s a   e   i s o t e r m i c a

Passo 2

Vamos primeiro observar a parede do forno A , devido a consideração I que fizemos no passo 1 temos:

ε A = ε f = α A = 0,85

Assim a potência emissiva é:

E A = ε A E b T f 4 = ε A σ T f = 0,85 ⋅ 5,67 ⋅ 10 - 8 ⋅ 3000 4

E A = 3,904 ⋅ 10 6   W m 2

Como o forno é isotérmico em relação a vizinhança, podemos aceitar a consideração de corpo negro, assim:

G A = J A = E b T f = σ ⋅ T f 4

5,67 ⋅ 10 - 8 ⋅ 3000 4 = 4,593 ⋅ 10 6   W m 2

Agora temos que do balanço de energia, de acordo com a equação 12.54 temos:

ρ λ + α λ + τ λ = 1

Ou seja:

α λ = 1 - ρ λ + τ λ

α 1 = 0,1 ,   α 2 = 0,3

Agora podemos calcular as características para o ponto B, assim:

α B = ∫ 0 ∞ α λ G λ d λ G = F 0 - λ T ⋅ α 1 + 1 - F 0 - λ T ⋅ α 2

Onde λ 1 T s = 5 ⋅ 3000 = 15000 μ m ⋅ K e da tabela 12.1   F 0 → λ T = 0,97

α B = 0,106

Agora temos que nossa emissividade é:

ε B = ∫ 0 ∞ ε λ E λ ,   b d λ E b ,   0 = F 0 - λ T ⋅ α 1 + 1 - F 0 - λ T ⋅ α 2

Onde λ 1 T s = 5 ⋅ 300 = 1500 μ m ⋅ K e da tabela 12.1   F 0 → λ T = 0,0138

ε B = 0,297

Passo 3

A potencia emissiva é dada por:

E B = ε B E b ,   B = 0,297 ⋅ 5,67 ⋅ 10 - 8   W m 2 ⋅ K 4 ⋅ 300   K 4

E B = 136,5   W m 2

A irradiação do ponto B é igual à do forno que é considerado um corpo negro devido ser muito maior que nosso ponto B é dada por:

G B = G A = σ T f 4 = 5,67 ⋅ 10 - 8   W m 2 ⋅ K 4 ⋅ 300   K 4

G B = 4,593 ⋅ 10 6   W m 2

Por fim temos que a radiosidade deixando o ponto B devido a emissão e a reflexão irradiativa é dada por:

J B = E B + ρ B ⋅ G B = 136,5 + 0,3 ⋅ 4,593 ⋅ 10 6   W m 2

J B = 1,378 ⋅ 10 6 W m 2

Isso é tudo pessoal! \o/

Resposta

α B = 0,106 , ε B = 0,297 , E B = 136,5   W m 2 , G B = 4,593 ⋅ 10 6   W m 2 e J B = 1,378 ⋅ 10 6 W m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma placa opaca horizontal bem isolada nas bordas e na superfície inferior. A placa é uniformemente irradiada de cima enquanto o ar a T ∞ = 300 K flui sobre a superfície, fornecendo um coefi
A emissividade de uma superfície revestida de óxido de alumínio pode ser aproximada como 0,15 para radiação em comprimentos de onda menores que 5 μ m e como 0,9 para radiação em comprimentos de onda s
A função de emissividade espectral de uma superfície opaca a 1000 K é aproximada como: ε λ = ε 1 = 0,4 , 0 ≤ λ3μ m ε 2 = 0,7 ,3μ m ≤ λ6μ m ε 3 = 0 , 3 ,6μ m ≤ λ∞ Determine a emissividade média da supe
Uma pequena superfície de área A 1 = 5 cm2 emite radiação como um corpo negro a T 1 = 1000 K. Um sensor de radiação de área A 2 = 3 cm2 é colocado na direção normal da visualização da superfície A 1 n
A emissividade de um filamento de tungstênio pode ser aproximada como 0,5 para radiação em comprimentos de onda menores que 1 μ m e 0,15 para radiação superior a 1 μ m. Determine a emissividade média