Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 9
De acordo com sua distribuição direcional, a radiação solar que incide sobre a superfície terrestre pode ser dividida em duas parcelas. A parcela direta, que é constituída por raios paralelos que incidem em um ângulo de zênite fixo , e a parcela difusa, formada por radiação que pode ser aproximada como sendo distribuída de forma difusa em relação a .
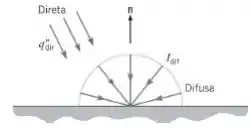
Considere condições de céu claro nas quais a radiação direta incide com um ângulo com um fluxo total (com base na área normal aos raios) de , e com uma intensidade total da radiação difusa Qual é o valor da irradiação solar total na superfície terrestre?
Passo 1
Oi oi oiii, vamos para mais uma?? Nessa questão nós temos o fluxo e a intensidade de componentes diretos e difusos, respectivamente, de irradiação solar. Com isso, vamos calcular a irradiação total, show?
Passo 2
Como a irradiação é baseada na área superficial real, a contribuição devido à radiação solar direta é:
E a contribuição devido à radiação difusa é:
Então,
Passo 3
Substituindo os valores ficamos com:
Que é o que a questão nos pediu. 😊