Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 14

Uma pequena fonte de calor radiante com área A 1   = 2   ×   10 – 4   m 2 emite difusamente com uma intensidade I 1   =   1000   W / ( m 2 · s r ) . Uma segunda área pequena,   A 2   =   1 ×   10 – 4   m 2 está localizada como mostrado no esboço a seguir.

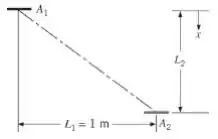
(a) Determine a irradiação de A 2 para L 2   =   0,5   m .

(b) Represente graficamente A 2 no intervalo 0   ≤   L 2   ≤   10   m .

Passo 1

Nessa questão nós temos a área de superfície e emissão da área A 1 e o tamanho e orientação da área A 2 . E com isso queremos determinar a irradiação de A 2 para L 2   =   0,5   m , beleza?

Passo 2

Para resolver essa questão vamos assumir emissão difusa. A irradiação da superfície 1 é G 1 - 2   =   q 1 - 2   / A 2     e do exemplo 12.1,

q 1 - 2   = I 1 A 1 cos ⁡ θ 1 ω 2 - 1 = I 1 A 1 cos ⁡ θ 1 A 2 cos ⁡ θ 2 r 2

Como,

θ 1 = θ 2 = θ = tan - 1 ⁡ L 1 L 2 = tan - 1 ⁡ 1 0,5 = 63,43 °

E,

r 2 = L 1 2 + L 2 2 = 1 m 2 + 0,5 m 2 = 1,25 m 2

Passo 3

Temos que,

G 1 - 2 = I 1 A 1 cos 2 ⁡ θ r 2

E substituindo os valores,

G 1 - 2 = 1000 W m 2 · s r × 2   ×   10 – 4   m 2 × cos 2 ⁡ ( 63,43 ° ) 1,25 m 2

G 1 - 2 = 0,032   W / m 2

Resposta

  1. G 1 - 2 = 0,032   W / m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pequena superfície de área emite radiação com uma intensidade que pode ser expressa como I θ , ϕ = 100ϕ cos ⁡ θ , onde I tem unidades de W/m².sr Determine o poder emissivo da superfície para o hem
Uma pequena superfície de área A1 = 3 cm² e um sensor de radiação com área A2 = 1 cm² são orientados como mostrado na figura abaixo. A superfície A1 é opaca e mantém uma temperatura constante de T1 =
Considere uma pequena superfície negra de área A = 3,5 cm² mantida a 750 K. Determine a taxa em que a energia de radiação é emitida pela superfície através da abertura em forma de anel, definida por 0
Um sensor de radiação e uma pequena superfície de área A1, ambos emitentes de radiação do corpo negro, são orientados como mostra a figura abaixo. Determine a distância L onde o sensor mede 2/3 da tax
Um recipiente tem uma área superficial interna de 100 m2 , e esta superfície, que é mantida a uma temperatura constante, é preta. Uma pequena abertura no recipiente tem uma área de 0,02 m2 . A taxa de