Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 118

Considere que o receptor central do Problema 12.117 seja uma casca cilíndrica com diâmetro externo D = 7 m e comprimento L = 12 m. A superfície externa é opaca e difusa, com uma absortividade espectral de αλ = 0,9 para λ 3 μm. Esta superfície está exposta ao ar ambiente quiescente, com T∞ = 300 K.

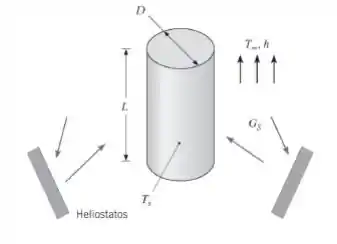
  1. Considere condições de operação representativas nas quais irradiação solar com GS = 80.000 W/m2 está uniformemente distribuída ao longo da superfície receptora, que se encontra a uma temperatura de Ts = 800 K. Determine a taxa na qual a energia é coletada pelo receptor e a eficiência do coletor correspondente.
  2. A temperatura superficial é afetada pelas condições internas no receptor. Para GS = 80.000 W/m2 , calcule e represente graficamente a taxa de coleta de energia e a eficiência do coletor para 600 ≤ Ts ≤ 1000 K.

Passo 1

Fala aí! Temos duas letrinhas para resolver… Mas antes de tudo precisaremos de uns dados a mais, podemos pegar eles na tabela A-4, usando um T f = 550   K :

v = 45,6   .   10 - 6   m ² / s k = 0,0439   W / m . K

α = 66,7   .   10 - 6   m ² / s P r = 0,683

Beleza!

Vamos começar pela letra a, ok?

Nossa questão quer a taxa na qual a energia é coletada pelo receptor e a eficiência do coletor, partiu encontrar então!

Começando pela taxa, podemos usar essa equação aqui, olha só:

q = A s   .   α S   .   G S   -   E   -   q c o n v "

E separando a equação de cada termo aí teremos:

A s = π   .   D   .   L E = ε   .   σ   .   T s 4 q c o n v " = h _   .   T s - T ∞

Substituindo esses caras aí, vamos ficar com:

q = π   .   D   .   L   .   α S   .   G S   -   ε   .   σ   .   T s 4   -   h _   .   T s - T ∞

Passo 2

Ops! Temos que encontrar alguns fatores aí pra depois substituir, então vamos lá! Vamos escrever quem está faltando: α S , ε e h _ … Beleza! Agora vamos achar eles:

α S = α 1   .   F 0 → λ + α 2   .   1 - F 0 → λ

Pra achar esse F 0 → λ , considerando T = 5800   K , precisamo fazer o seguinte:

λ   .   T   =   3   .   5800

λ   .   T   =   17400   μ m . K

Aí é só a gente ir lá na tabela 12.2 e temos que:

F 0 → λ = 0,979

Então encontraremos:

α S = 0,9   .   0,979 + 0,2   .   1 - 0,979

α S = 0,885

Agora vamos encontrar a emissividade, belê?

ε =   ε 1   .   F 0 → λ   +   ε 2   .   1 - F 0 → λ

Se liga aqui que é um bizu importante! esse F 0 → λ não é o mesmo da absortividade, ok?

Porque a temperatura que vamos usar é o T s , vamos achar ele então:

λ   .   T   =   3   .   800

λ   .   T   =   2400   μ m . K

Indo lá na tabela 12.2 e teremos:

F 0 → λ = 0,140

E nossa emissividade será:

ε =   0,9   .   0,140   +   0,2   .   1 - 0,140

ε =   0,298

Show de bolinhas! Mas ainda falta mais um…

Passo 3

Agora só falta achar o h _ , vamos nessa!

h _ = N u _ L   .   k L

E podemos achar o N u _ L assim:

N u _ L = 0,825   +   0,387   .   R a L 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

Ops! Ainda falta alguém… Vamos nele então:

R a L = g   .   β   .   T s - T ∞   .   L ³ α   .   v

R a L = 9,8   .   1 550   .   500   .   12 ³ 66,7   .   10 - 6   .   45,6   .   10 - 6

R a L = 5,06   .   10 12

Agora sim, vamos voltar ali em cima:

N u _ L = 0,825   +   0,387   .   5,06   .   10 12 1 / 6 1 + 0,492 12 9 / 16 8 / 27 2

N u _ L = 1867

Aeee, vamos agora achar o h _ :

h _ = 1867   .   0,0439 12

h _ = 6,83   W / m ² . K

E finalmente teremos taxa de calor:

q = π   .   7   .   12   .   0,885   .   80000   -   0,298   .   5,67   .   10 - 8   .   800 4   -   6,83   .   500

q = 1,60   .   10 7   W

Show! Agora só falta achar a eficiência!

Passo 4

Bom, pra achar a eficiência vamos fazer o seguinte:

η = q A s   .   G s

η = 1,60   .   10 7 π   .   7   .   12   .   80000

η = 0,758

Uhull! Arrasamos!

Resposta

  1. q = 1,60   .   10 7   W e η = 0,758

  2. Precisa do uso de software.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma superfície cinza e opaca, cuja absortividade direcional é de 0,8 para 0 ≤ θ ≤ 3 0 ° e de 0,1 para θ3 0 ° . A superfície é horizontal e está exposta à irradiação solar com os componentes
Um termopar cuja superfície é difusa e cinza, apresentando uma emissividade de 0,6 , indica uma temperatura de 180 ° C quando é utilizado para medir a temperatura de um gás que escoa através de um gra
Um pequeno disco com 4m m de diâmetro está posicionado no centro de uma cúpula hemisférica isotérmica. O disco é difuso e cinza com uma emissividade de 0 , 8 e é mantido a 10 00K . A cúpula hemisféric
A absortividade direcional de uma superfície cinza varia com θ como a seguir.(a) Qual é a razão entre a absortividade normal α n e a emissividade hemisférica da superfície? (b) Considere uma placa com
A absortividade espectral do alumínio revestido por uma fina camada de dióxido de silício pode ser aproximada por α λ , 1 = 0,98 para λλ c e α λ , 2 = 0,05 para λ ≥ λ c , sendo o comprimento de onda d