Adicione à sua linha de Rayleigh do problema 9.110 uma linha de Fanno (ver problema 9.94) para entalpia de estagnação igual ao valor associado ao estado 1 no Problema 9.110. As duas curvas se interceptarão no estado 1, que é subsônico, e em um certo estado 2, que é supersônico. Interprete esses dois estados em face da tabela B.2
Passo 1
Bem, primeiramente como você está?! Espero que esteja tudo tranquilo por aí pra gente seguir para mais um desafio da mecflu e termodinâmica aplicada
Vamos relembrar as condições de referência que nos foram dadas lá no nosso problema 9.110?
A temperatura de estagnação é calculada como sendo:
Nos outros lugares, a temperatura será dada por:
Passo 2
Ainda do nosso problema 9.110, temos que e
Então vamos lá, mais uma vez variando V, conseguiremos computar os valores de T, e s. Plotamos depois uma linha de Fanno na nossa curva anterior feita no P9.110, se liga como ficaria!!!
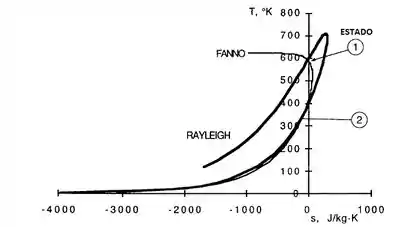
Passo 3
Vamos fazer uns comentários agora: A interseção subsônica é o estado 1, onde e . Por sua vez, a região supersônica é quando onde por exemplo temos que a temperatura está em torno de 316 K. Esses dois pontos correspondem ao que chamamos de normal da onda de choque, onde “2” é a condição supersônica e “1” a condição subsônica. Podemos confirmar esses dados pela tabela B.2 do livro, onde mostra que com Ma = 2,2 temos uma razão de temperatura em torno de 1,857. O que diz que nos nossos dados quando fazemos as contas verificamos que temos uma razão de 588K/316K = 1,86, o que está perfeitamente com concordância com os dados)
Resposta
Ei, a resposta está no passo a passo :)