Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 11

Desprezando os atritos no pistão da figura, determinar:

  1. A potência da bomba em k W se seu rendimento for 80 % ;
  2. A força que o pistão pode equilibrar com a haste.

Dados: A 2 = A 3 = A 4 = A 5 = A 6 = 10   c m 2 ; A G 3 = 8   c m 2 ; A p = 20   c m 2 ; A b = 10   c m 2 ; H p 1,2 = H p 3,4 = 0,5   m ; H p 4,5 = 0   m ; H p 5,6 = 1   m ; g = 10 m s 2 ; γ = 10 4   N / m 3 . Supor o cilindro no plano da tubulação.

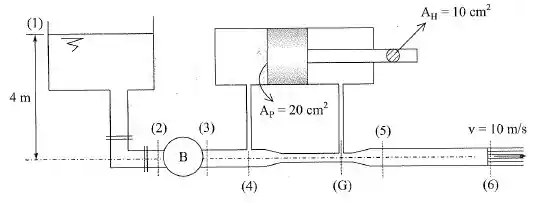
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como as áreas das seções 2 ,   3 ,   4 ,   5   e 6 são iguais, pelo principio da continuidade, podemos inferir que as velocidades nessas seções também são iguais, pois a vazão é constante. Portanto:

v 2 = v 3 = v 4 = v 5 = v 6 = 10   m / s

Podemos então descobrir a velocidade na garganta. Como a vazão é igual em todo o sistema, temos que:

Q 6 = Q G

v 6 A 6 = v G A G

v G = A 6 A G v 6

Substituindo os valores temos que:

v G = 10 8 10

v G = 12,5   m / s

Passo 2

Descobertas as velocidades, podemos aplicar a equação de Bernoulli entre os pontos 1 e 6 . Note que no sistema temos uma máquina atuando (bomba) e também há perdas de carga. Portanto, teremos:

H 1 + H B = H 6 + H p 1,6

z 1 + v 1 2 2 g + P 1 γ + H B = z 6 + v 6 2 2 g + P 6 γ + H p 1,6

Para o ponto 1 só teremos carga gravitacional, pois a velocidade no ponto é considerada nula e a pressão relativa também.

Para o ponto 6 , podemos considerar a cota z 6 = 0 , e a pressão relativa, por estar ao ar livre também é nula, logo:

z 1 + 0 + 0 + H B = 0 + v 6 2 2 g + 0 + H p 1,6

Substituindo os valores conhecidos, temos que:

4 + H B = 100 20 + H p 1,6

A perda de carga entre os pontos 1 e 6 é dada por:

H p 1,6 = H p 1,2 + H p 2,3 + H p 3,4 + H p 4,5 + H p 5,6

H p 1,6 = 0,5 + 0 + 0,5 + 0 + 1

H p 1,6 = 2   m

Portanto, a carga da bomba é dada por:

H B = 5 + 2 - 4

H B = 3   m

Passo 3

A potência da bomba pode ser calculada por:

N B = γ H B Q η

Calculando, temos que:

N B = 10 4 3 10 ⋅ 10 - 3 0,8

N B = 375   W

Ou:

N B = 0,375   k W

Passo 4

Para o item b vamos aplicar Bernoulli entre os pontos 1 e 4 :

H 1 + H B = H 4 + H p 1,4

z 1 + v 1 2 2 g + P 1 γ + H B = z 4 + v 4 2 2 g + P 4 γ + H p 1,4

Para o ponto 1 só teremos carga gravitacional, pois a velocidade no ponto é considerada nula e a pressão relativa também.

Para o ponto 4 , podemos considerar a cota z 4 = 0 , logo:

z 1 + 0 + 0 + H B = 0 + v 4 2 2 g + P 4 γ + H p 1,4

Substituindo os valores conhecidos, temos que:

4 + H B = 100 20 + P 4 10 4 + H p 1,4

A perda de carga entre os pontos 1 e 4 é dada por:

H p 1,4 = H p 1,2 + H p 2,3 + H p 3,4

H p 1,4 = 0,5 + 0 + 0,5

H p 1,4 = 1   m

Portanto, temos que a pressão em 4 é dada por:

4 + 3 = 5 + P 4 10 4 + 1

P 4 = 10 4   P a

Passo 5

Agora vamos aplicar Bernoulli entre os pontos 1 e G :

H 1 + H B = H G + H p 1 , G

z 1 + v 1 2 2 g + P 1 γ + H B = z G + v G 2 2 g + P G γ + H p 1 , G

Para o ponto 1 só teremos carga gravitacional, pois a velocidade no ponto é considerada nula e a pressão relativa também.

Para o ponto 4 , podemos considerar a cota z G = 0 , logo:

z 1 + 0 + 0 + H B = 0 + v G 2 2 g + P G γ + H p 1,4

Substituindo os valores conhecidos, temos que:

4 + H B = 156,25 20 + P G 10 4 + H p 1 , G

A perda de carga entre os pontos 1 e 4 é dada por:

H p 1 , G = H p 1,2 + H p 2 , 3 + H p 3,4 + H p 4,5

H p 1 , G = 0,5 + 0 + 0,5 + 0

H p 1 , G = 1   m

Portanto, temos que a pressão em 4 é dada por:

4 + 3 = 7,8125 + P G 10 4 + 1

P G = - 1,8125 ⋅ 10 4   P a

Passo 6

Agora podemos encontrar a força na haste. Ela é dada pela equação de equilíbrio do pistão. As forças do lado esquerdo devem ser iguais às forças do lado direito. Temos que:

F P 4 = F P G + F

Como a força é o produto da pressão pela área de contato, temos que:

F P 4 = P 4 A P

E:

F P G = P G A P - A H

Temos que subtrair as áreas pois a pressão da garganta não age em toda a área do pistão. Portanto, temos que:

F = P 4 A P - P G A P - A H

F = 10 4 20 ⋅ 10 - 4 - - 1,8125 ⋅ 10 4 20 ⋅ 10 - 4 - 1 0 ⋅ 10 - 4

F = 38,1   N

Resposta

a )     N B = 0,375   k W

b )   F = 38,1   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque pressurizado de água tem um orifício de 10c m de diâmetro na parte inferior, onde a água é descarregada para a atmosfera. O nível da água está 3m acima da saída. A pressão do ar do tanque ac
O diâmetro de um tanque de água cilíndrico é D 0 e sua altura é H . O tanque é enchido com água e está aberto para a atmosfera. Um orifício de diâmetro D com uma entrada uniforme (ou seja, sem perdas)
Um avião voa a uma altitude de 12.000 m . Determine a pressão manométrica no ponto de estagnação no nariz do avião se a velocidade for de 200k m / h . Como você solucionaria este problema para uma vel
A água entra em um tanque com diâmetro D , de forma constante a uma vazão de massa de m e ˙ . Um orifício na parte inferior com diâmetro D 0 permite que a água escape. O orifício tem uma entrada arred
Reconsidere o Problema 5 - 46 . Determine em quanto tempo a piscina será esvaziada completamente.