Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 9

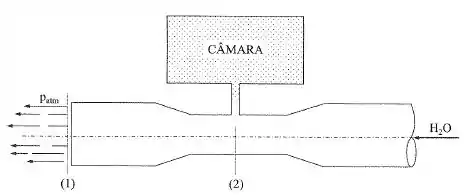
Um dos métodos para se produzir vácuo numa câmara é descarregar água por um tubo convergente-divergente, como é mostrado na figura. Qual deve ser a vazão em massa de água pelo convergente-divergente, para produzir uma depressão de 22   c m de mercúrio na câmara da figura? Dados: desprezar as perdas de carga; γ H 2 O = 10 4   N / m 3 ; γ H g = 1,36 × 10 5   N / m 3 ; g = 10   m / s 2 ; D 1 = 72   m m ; D 2 = 36   m m .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão… O enunciado está pedindo a vazão em massa de água, ok? Vamos lá!

Ele nos disse que existe uma depressão de 22   c m H g . Uma depressão quer dizer uma pressão negativa, logo:

P 2 =   - γ H g H H g

Substituindo nossos dados:

P 2 =   - 1,36 ⋅ 10 5 ⋅ 22 ⋅ 10 - 2

P 2 =   - 29920   P a

Usando agora a equação de Bernoulli, temos que:

H 2 = H 1

No ponto 2 temos carga de pressão e cinética, e no ponto 1 apenas carga cinética, portanto:

v 2 2 2 g + P 2 γ = v 1 2 2 g

Passo 2

A equação da continuidade nos diz que:

ρ v 1 A 1 = ρ v 2 A 2

Logo:

v 1 ⋅ π 4 ⋅ D 1 2 = v 2 ⋅ π 4 ⋅ D 2 2

v 2 = D 1 2 D 2 2 ⋅ v 1

Substituindo nossos dados, temos:

v 2 = 72 2 36 2 ⋅ v 1

v 2 = 4   v 1

Aplicando isso na equação de Bernoulli que vimos no passo anterior, vamos ficar com:

4   v 1 2 2 g + P 2 γ = v 1 2 2 g

Sendo assim, podemos encontrar v 1 , substituindo todo mundo que temos:

16 v 1 2 20 + - 29920 10 4 = v 1 2 20

Resolvendo, temos que:

v 1 = 2   m / s

Show! Então a vazão mássica será:

Q m 1 = γ g ⋅ v 1 ⋅ A 1

Q m 1 = 10 4 10 ⋅ 2 ⋅ π 4 72 ⋅ 10 - 3 2

Q m 1 = 8,14   k g / s

Prontinho!

Resposta

Q m 1 = 8,14   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Problema 5-19. Usando o aplicativo EES (ou outro), investigue o efeito da velocidade do vento e o diâmetro de abrangência da lâmina sobre a geração de potência eólica. Faça a velocidade
Determinar a velocidade do jato do líquido no orifício do tanque de grandes dimensões da figura. Considerar fluido ideal.
A velocidade de um líquido que escoa em um tubo circular de raio R varia de zero na parede até o máximo no centro do tubo. A distribuição da velocidade no tubo pode ser representada por V r , onde r é
Uma turbina hidráulica tem 85m de carga disponível a uma vazão de 0,25m 3 / s , e sua eficiência geral de turbina-gerador é de 78 % . Determine a energia elétrica resultante dessa turbina.
A água entra em uma turbina hidráulica por meio de um tubo com 30c m de diâmetro a uma vazão de 0,6m 3 / s e sai através de um tubo com 25c m de diâmetro. A queda de pressão na turbina é medida por um