Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 8

No conduto da figura, o fluido é considerado ideal.

Dados: H 1 = 16   m ; P 1 = 52   k P a ; γ = 10 4   N / m 3 ; D 1 = 10   c m .

Determinar:

  1. A vazão em peso;
  2. A altura h 1 no manômetro;
  3. O diâmetro da seção ( 2 ) .

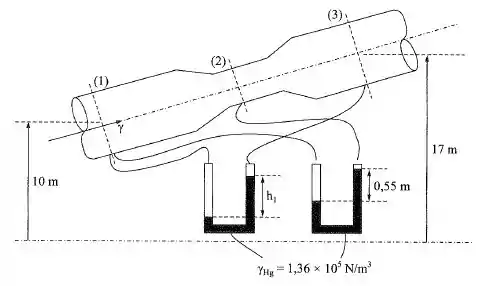
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos deu a carga total no ponto 1 . Podemos então descobrir a velocidade no ponto 1 :

H 1 = z 1 + v 1 2 2 g + P 1 γ

16 = 10 + v 1 2 2 g + 5,2

Logo:

v 1 = 4   m / s

Sabendo a velocidade podemos calcular a vazão em peso que é dada por:

Q G = γ ⋅ v ⋅ A

Substituindo os valores, temos que:

Q G = 10 4 ⋅ 4 ⋅ π 4 0,1 2

Q G = 314,2   N / s

Passo 2

Como o fluido é ideal, podemos a partir da equação da continuidade, afirmar que a velocidade no ponto 3 é a mesma que no ponto 1 pois as seções são iguais.

v 1 = v 3

Por Bernoulli sabemos que a carga total deve ser igual em todas as seções, logo:

H 1 = H 2 = H 3

Portanto:

H 3 = z 3 + v 3 2 2 g + P 3 γ

16 = 1 7 + 16 20 + P 3 10 4

Logo:

P 3 = - 18   k P a

De posse desse dado podemos encontrar a altura h 1 a partir da equação manométrica:

P 1 + γ h 1 = P 3 + γ H g h 1 + γ ⋅ 7   m

h 1 γ H g - γ = P 1 - P 3 - 7 ⋅ 10 4

Resolvendo, temos que:

h 1 1,36 ⋅ 10 5 - 10 4 = 52 ⋅ 10 3 - - 18 ⋅ 10 3 - 7 ⋅ 10 4

h 1 = 0 1,26 ⋅ 10 5

Logo:

h 1 = 0   m

Passo 3

Aplicando a equação manométrica no segundo caminho podemos descobrir a pressão em 2 .

Temos que:

P 1 + 0,55 γ = P 2 + z 2 - 10 γ + 0,55 γ H g

Resolvendo, encontramos que:

P 2 = 82700 - 10000 z 2

Aplicando Bernoulli, temos que:

z 1 + v 1 2 2 g + P 1 γ = z 2 + v 2 2 2 g + P 2 γ

Substituindo os valores conhecidos temos que:

10 + 0,8 + 5,2 = z 2 + v 2 2 2 g + 82700 - 10000 z 2 10 4

16 = z 2 + v 2 2 2 g + 8,27 - z 2

Como podemos ver o valor de z 2 não precisou ser calculado, logo:

v 2 = 12,43   m / s

E aplicando a equação da continuidade, temos que:

v 1 A 1 = v 2 A 2

v 1 π 4 D 1 2 = v 2 π 4 D 2 2

Logo, temos que:

D 2 = v 1 v 2 D 1 2

D 2 = 4 12,43 0,1 2

D 2 = 5,7   c m

Resposta

a ) Q G = 314   N / s  

b )   h 1 = 0

c )   D 2 = 5,7   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar a 4,18k g / m 3 entra em um bocal que tem relação entre área de entrada e saída de 2 : 1 com uma velocidade de 120m / s e sai com uma velocidade de 380m / s . Determine a densidade do ar na saída.
O nível da água em um tanque é de 20m acima do solo. Uma mangueira está conectada à parte inferior do tanque, e o bocal no final da mangueira aponta diretamente para cima. O tanque está no nível do ma
Um tanque com diâmetro D 0 = 10m inicialmente está cheio com água até 2m acima do centro de uma válvula com diâmetro D = 10c m próxima à parte inferior. A superfície do tanque está aberta para a atmos
A água escoa a uma vazão de 20L / s através de um tubo horizontal cujo diâmetro de uma válvula do tubo é medida como 2k P a . Determine a perda de carga irreversível da válvula, e a potência de bombea
Água subterrânea está sendo bombeada para uma piscina cuja seção transversal tem 3m× 4m enquanto a água é descarregada através de um orifício com 5c m de diâmetro à velocidade média constante de 5m /