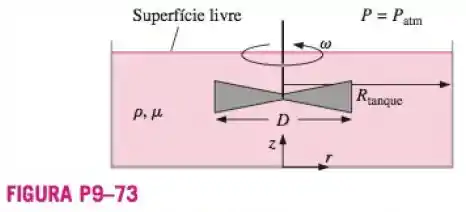
Um agitador mistura produtos químicos em um grande tanque (Fig. P9–73). A superfície livre do líquido é exposta ao ar ambiente. Os efeitos da tensão superficial são insignificantes. Discuta as condições de contorno necessárias para resolver esse problema. Especificamente, quais são as condições de contorno de velocidade em termos das coordenadas cilíndricas e componentes de velocidade em todas as superfícies, incluindo as pás e a superfície livre? Que condições de contorno de pressão são apropriadas para esse campo de escoamento? Escreva as equações matemáticas para cada condição de contorno e discuta.

Por aqui a gente não paaara !!

Precisamos de condições de contorno para a velocidade, certo?

Então para isso nós faremos algumas considerações!!

Segundo a condição de limite antiderrapante, as paredes do tanque são estacionárias, ou seja:

Se a velocidade é zero devido ao estado estacionário:

Também observamos isso na parede inferior do tanque, certo? Já que o mesmo caso se aplica aí também. Portanto, quando , teremos:

Beleza até aqui?

Levando em conta a mesma condição, nas superfícies das pás a velocidade deve ser igual a velocidade que a mesma possui !

Como as pás não se movem na direção radial ou na direção vertical, teremos que as componentes da velocidade nestes casos será:

Então a única componente da velocidade diferente de zero será:

Se lembram lá da física? Pois é !!

Achamos as condições de contorno para a velocidade !!