Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 69

Investigue o potencial complexo f z = A cosh ⁡ [ p ( z / a ) ]   e trace as linhas de corrente dentro da região mostrada na Figura P 8.69 . Que palavra hifenizada (de origem francesa) pode descrever tal padrão de escoamento?

Passo 1

E aí, tudo bem? Bora matar essa questão!

Antes de tudo vamos separar nossas funções potenciais!

Usando como base a tabela 8.2 para um corpo dipolo, temos:

ψ = A senh ⁡ ψ x a ⋅ sen ⁡ π y a

ϕ = A cos h ⁡ ψ x a ⋅ cos ⁡ π y a

Passo 2

Bem, agora temos que esquematizar nosso problema

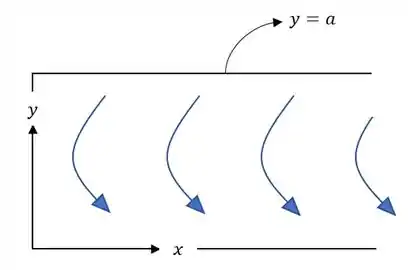
Bem, baseado nas equações o padrão vai se repetir para os intervalos continuamente para múltiplos naturais de a , assim:

i n t .   R e p e t i ç ã o = { a < y < 2 a ; 2 a < y < 3 a ; 3 a < y < 4 a … }

Assim o escoamento se comporta como um “beco sem saída’

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

ψ = A senh ⁡ ψ x a ⋅ sen ⁡ π y a

ϕ = A cosh ⁡ ψ x a ⋅ cos ⁡ π y a

Bem, baseado nas equações o padrão vai se repetir para os intervalos continuamente para múltiplos naturais de a , assim:

i n t .   R e p e t i ç ã o = { a < y < 2 a ; 2 a < y < 3 a ; 3 a < y < 4 a … }

Assim o escoamento se comporta como um “beco sem saída’

Desenho vide passo a passo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para cada uma das equações listadas, escreva a equação em forma vetorial e decida se ela é linear ou não-linear.Se ela for não-linear, que termo(s) a faz(em) ser assim?(a) equação da continuidade inco
Considere o escoamento permanente, bidimensional, incompressível no plano x z em vez do plano x y .Na Figura P9-103 são mostradas curvas com função corrente constante. As componentes de velocidade dif
Simplifique a equação de Navier-Stokes o máximo possível para o caso de um líquido incompressível que está sendo acelerado como um corpo rígidoem uma direção arbitrária (Fig. P9-120).A gravidade age n
Simplifique a equação de Navier-Stokes o máximo possível para o caso dehidrostáticasincompressíveis,com a gravidade atuando nadireçãonegativa de z .Comece com a forma vetorial incompressível da equaçã
Aproximamos o escoamento do ar para dentro do acessório de piso, de um aspirador de pó por uma função corrente ψ = - V ˙ 2 π L arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b 2 / r 2 no plano central (o plano x y )