Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 77
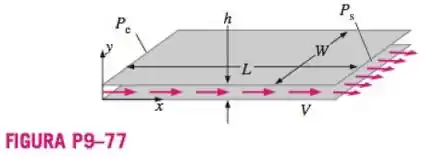
O óleo de motor à temperatura é forçado entre duas placas planas paralelas, permanentes, muito grandes separadas por um espaçamento de altura (Fig. P9-77). As dimensões da placa são e . A pressão de saída é a pressão atmosférica, a pressão de entrada é de 1 atm manométrica. Estime a vazão em volume de óleo. Calcule também o número de Reynolds do fluxo de óleo, com base na altura h e velocidade média . O escoamento é laminar ou turbulento?
Passo 1
Sinto cheiro de questão boa aqui ein !!
Animados para começar?
Boom, vamos assumir aqui que o escoamento é permanente, incompressível e totalmente desenvolvido, ok?
E mais uma coisa!! Podemos assumir que o fluido está escoando ao longo do eixo x, certo?
Portanto, não vai haver velocidade na direção y!!
Se não temos velocidade na direção y, o fluxo de óleo pode ser calculado como:
Vamos precisar achar tanto quanto , certo?
Vamos começar pelo Uma área diferencial será dada em função da largura e da variação de y:
E a velocidade na direção x,
Para o caso de um escoamento completamente desenvolvido, em duas dimensões ao longo de duas placas paralelas:
Agora que temos tudo o que precisamos podemos colocar na integral, certo?
Mas não se esqueçam, o y aqui varia de zero até a altura entre as placas:
Tirando da integral o que não varia com o y:
E integrando:
Passo 2
Agora precisamos dar nomes aos bois!!
Olhando a Tabela A.7 para o óleo de motor a 60°C:
O problema nos disse que:
A única coisa que ainda não é o valor para Mas nós temos uma fórmula para isso, querem ver?
Vamos ver o que o problema nos deu?
Bora substituir?
Substituindo na fórmula do Passo 1:
Passo 3
Leegal !! Achamos uma das respostas, mas ainda precisamos achar a velocidade, não é?
Se lembram como a velocidade se relaciona com o fluxo?
A área da seção transversal do escoamento é dado pela largura vezes a altura do canal:
Substituindo:
E chegamos ao fim de mais uma, galerinhaa !!