Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 62

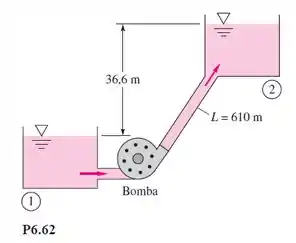
Água a 20°C deve ser bombeada por um tubo de 610 m do reservatório 1 para o reservatório 2 a uma taxa de 85 L/s, como mostra a Figura P6.62. Se o tubo é de ferro fundido de 150 mm de diâmetro e a bomba tem 75% de rendimento, qual é a potência necessária, em hp, para a bomba?

Passo 1

Bora lá pra mais uma, família!

Para a água, já sabemos, ρ = 998   k g / m 3 e μ = 0,001   k g / ( m ⋅ s ) , transformando a vazão, teremos Q = 0,085   m 3 / s . Assim, calculando a velocidade:

V = Q A = 0,085 m 3 s π 4 0,150   m 2 = 4,81   m / s

Agora, calculando Reynolds,

R e = ρ V D μ = 998 k g m 3 4,81 m s 0,150   m 0,001   k g / ( m ⋅ s ) = 720000

Temos que, para o ferro fundido, sua rugosidade relativa será:

ϵ D = 0,26 m m 150 m m = 0,00173

Assim, pelo Diagrama de Moody, encontraremos o seguinte fator de atrito:

f = 0,023

Passo 2

Beleza, agora faremos a equação de energia, assim:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h f + h b o m b a

Temos que ambos os tanques estão abertos a atmosfera, assim, as pressões irão se cortar. Temos também que na superfície ambas as velocidades se aproximam de zero, logo, nossa equação de energia ficará da seguinte maneira:

h b o m b a = Δ z + h f

Sendo,

h f = f L D V 2 2 g

Assim,

h b o m b a = Δ z + f L D V 2 2 g

Substituindo,

h b o m b a = 36,6   m + 0,023   610   m 0,150   m 4,81 m s 2 2 9,81 m s 2 = 147   m  

Passo 3

Para encontrar a potência da bomba, teremos:

P = ρ g Q h b o m b a η = 998 k g m 3 9,81 m s 2 0,085 m 3 s 147   m 0,75 = 163,1   k W = 218,7   h p

Prontin!

Resposta

218,7   h p

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o escoamento de uma corrente uniforme paralela a uma placa plana aguda, a transição para uma camada limite turbulenta sobre a placa ocorre para Rex = rhoUx/mu = E6, em que U é a velocidade de apr
Um refrigerante à base de cola, aproximado como água pura a 20oC, preenche um recipiente de 240 ml por um tubo de 5 mm de diâmetro. Calcule o tempo mínimo de preenchimento se o escoamento no tubo se m
Mostre que, se a Equação (6.33) é precisa, a posição no escoamento turbulento em um tubo em que a velocidade local u se iguala à velocidade média V ocorre exatamente em r = 0,777 R , independentemente
Mercúrio a 20°C escoa por 4 m de tubo de vidro de 7 mm de diâmetro a uma velocidade média de 5 m/s. Calcule a perda de carga em metros e a queda de pressão em kPa.
Querosene a 20°C é bombeado a 0,15m 3 / s por 20 km de tubo horizontal de ferro fundido de 16 cm de diâmetro. Calcule a potência necessária de entrada em kW, se as bombas têm 85% de rendimento.