Para o escoamento de uma corrente uniforme paralela a uma placa plana aguda, a transição para uma camada limite turbulenta sobre a placa ocorre para Rex = rhoUx/mu = E6, em que U é a velocidade de aproximação e x é a distância ao longo da placa. Se U = 2,5 m/s, determine a distância x para os seguintes fluidos a 20°C e 1 atm:

(a) hidrogênio, (b) ar, (c) gasolina, (d) água, (e) mercúrio e (f) glicerina.

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 6.2 do livro, chamada “Escoamento interno e externo”.

Nesse problema, temos um escoamento uniforme em uma placa, onde a transição para a camada limite turbulenta sobre a placa ocorre para um número de Reynolds .

O número de Reynolds para esse escoamento pode ser calculado pela equação:

Sendo: a massa específica do fluido. a velocidade de aproximação do fluido com relação à placa; a distância ao longo da placa e a viscosidade dinâmica do fluido.

O enunciado quer a gente calcule distância ao longo da placa, e pra isso basta fazer para seis fluidos diferentes: hidrogênio, ar, gasolina, água, mercúrio e glicerina. Iremos considerar e a temperatura a e pressão atmosférica de .

Nessas condições, devemos buscar as propriedades dos fluidos nas Tabelas A.1, A.2, A.3 e A.4, disponíveis nas páginas 828 e 829 do livro. Sendo assim, podemos montar a seguinte tabela com a resolução do problema:

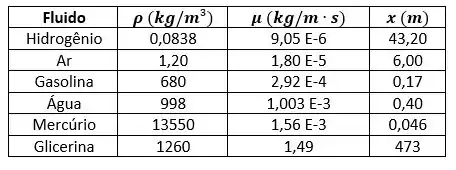
Como é possível notar pela tabela, quanto maior a massa específica , menor será a distância ao longo da placa e quanto maior maior será essa distância