Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 62
Água a 20°C descarrega para atmosfera padrão (nível do mar) através do bocal divisor abaixo. As áreas das seções são e . Se (absoluta) e vazão é , calcule a força sobre os parafusos dos flanges na seção 1.
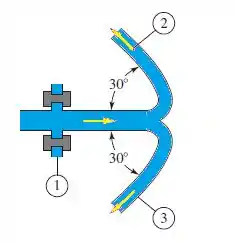
Passo 1
Aqui tem algo MARAVILHOSO que o enunciado já passou pra gente, que são os vários valores de área, pressão e vazão volumétrica! Isso nos ajudará em muitas coisas, porque por exemplo, a área transversal do ponto 2 e 3 são iguais, e suas vazões por consequência também são iguais, o que implicará que suas velocidades também serão iguais! Então, bora calcular!!
LEMBRETE: A vazão volumétrica foi dada em m³/h, precisamos então dividir por 3600s para obtermos a vazão em m³/s.
Outra coisa é, pelo balanço de massa a gente tem que:
Então a velocidade no ponto 1 é dada por:
Passo 2
Vamos agora fazer nosso volume de controle?
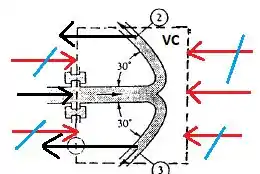
Note que todas as nossas pressões atmosféricas (em vermelho) estão se cancelando com seus pares na outra direção, com exceção do pedacinho que tem a entrada de fluido. Além disso, há outras duas forças que vão contribuir para nosso balanço de forças na direção x, que são oriundas das vazões de saída.
Vamos precisar decompor nossa velocidade de saída para obter sua componente x, que será dada por:
Passo 3
Agora vamos abrir nossas forças de pressão de tal forma que, se você se lembrar bem, as áreas de atuação da força de pressão atmosférica devem ser iguais a área de atuação da força p1, ou seja, podemos escrever de tal forma que: