Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 79

Ar a 20°C e 1 atm em um tubo entra no fundo de um medidor de vazão cônico de 85°, com um fluxo de massa de 0,3 kg/s, como mostra a Figura P3.79. O escoamento anular permanente é capaz de suportar um corpo cônico centrado, como mostra a figura. A velocidade do ar na aresta superior do corpo é igual à velocidade de entrada. Calcule o peso do corpo, em newtons.

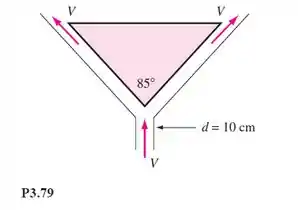
Passo 1

Bora pra mais uma!

Primeiramente, vamos achar a velocidade de entrada, temos a seguinte expressão para nos ajudar:

m ˙ = ρ a r A V → V = m ˙ ρ a r A

Já temos a vazão mássica da corrente, precisamos da massa específica, porque a área vamos conseguir calcular (temos o diâmetro), assim, para encontrar a massa específica:

ρ a r = p R T = 101325   P a 287 m 3 ⋅ P a k g ⋅ K 293   K = 1,205 k g m 3

Assim, substituindo na expressão para a velocidade:

V = 0,3 k g s 1,205 k g m 3 π 4 0,1   m 2 = 31,7   m / s

Passo 2

Agora, vamos usar o momento para encontrar o peso do corpo, assim, temos:

∑ F z = - W = m ˙ V cos ⁡ 42,5 ° - m ˙ V = m ˙ V ( cos ⁡ 42,5 ° - 1 )

Assim,

W = 0,3 k g s ⋅ 31,7 m s ⋅ 1 - cos ⁡ 42,5 ° = 2,49   N

Resposta

2,49 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dado o esquema da figura, sabendo que a seção do jato tem uma área de 520 cm² e que a área do pistão é 20 cm², determinar a vazão no bocal. Dados: γ H 2 O = 10 4N / m 3 ; γ H g = 1,36.10 5N / m 3 . Ob
Um fabricante de brinquedos constrói um carrinho impulsionado pelo ar de uma bexiga. No instante inicial em que é liberado o ar, determinar:a) a força de propulsão;b) a pressão do ar da bexiga, despre
Sabendo que o sistema da figura encontra-se em equilíbrio, desprezando as perdas, determinar a altura h 0 . ( γ H 2 O = 10 4N / m 3 ; γ = 2.10 4N / m 3 ; A p = 8.10 - 3m 2 ; h 1 = 78,5c m ; Q = 15,7L
No tanque da figura, determinar a força F s x que deve ser aplicada para que ele permaneça parado. Qual é o diâmetro do bocal que deverá ser instalado na parede oposta ao bocal mostrado na figura, par
Considerando que na região de escoamento completamente desenvolvido de um tubo, a integral da quantidade de movimento axial é a mesma em todas as seções transversais, explique a razão para a queda de