Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 82

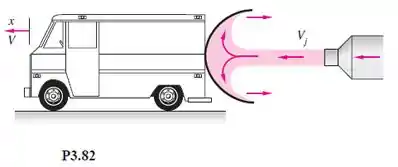
O modelo de carro da Figura P3.82 pesa 17 N e deve ser acelerado a partir do repouso por um jato de água de 1 cm de diâmetro à velocidade de 75 m/s. Desprezando o arrasto do ar e o atrito das rodas, calcule a velocidade do carro após um deslocamento de 1 m para a frente.

Passo 1

Simbora resolver essa!

Cara, o carro (nosso volume de controle) se movimenta para a esquerda na velocidade de aceleração, e temos o jato de água na velocidade relativa dada por V j - V . Vamos usar a equação 3.50 para resolver essa questão, temos:

∑ F x - ∫ a r e l a t i v a d m = 0 - m c a r r o a c a r r o = m ˙ s a í d a u s a í d a - m ˙ á g u a v o l t a n d o u á g u a v o l t a n d o = - 2 m ˙ j a t o d e á g u a ( V j - V )

Daí,

m c a r d V d t = 2 ρ A j V j - V 2  

Resolvendo essa equação diferencial, teremos o seguinte:

V = V j 2 Υ t 1 + V j Υ t

tendo, Υ = 2 ρ A j m c a r r o = 2 ρ A j P / g .

Passo 2

Resolvendo Υ , teremos:

Υ = 2 1000 k g m 3 π 4 0,01   m 2 17   N 9,81 m s 2 = 0,0906   m - 1

Substituindo na expressão de velocidade:

V = V j 2 0,0906 t 1 + V j 0,0906 t

O jato de velocidade está a V j = 75   m / s , assim:

V = 509 t 1 + 6,785 t

Passo 3

Encontramos uma equação para a velocidade em relação ao tempo. A nossa distância será dada por:

S = ∫ 0 t V d t

Calculando a distância, chegaremos a uma aceleração inicial de 509 m / s 2 , com isso, o carro irá atingir 1 m em um tempo de 0,072 s, alcançando uma velocidade de 24,6 m/s.

Resposta

24,6 m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O desviador de jato da figura move-se sobre o plano inclinado com velocidade de 1,0 m/s. Sabendo que seu peso é 200 N, que sua base é 1,0 m² e que entre o desviador e o plano inclinado existe uma cama
Calcular as componentes horizontal e vertical da força que o jato de água da figura exerce sobre o desviador. Dados: ρ = 1000k g / m 3 ; Q = 20L / s ; D j = 10c m . Desprezar a variação da seção do ja
Um propulsor a jato queima 1 kg/s de combustível. Calcular a força de propulsão, quando o avião voa à velocidade constante de 200 m/s. Dados: ρ a r = 1,2k g / m 3 ; ρ g a s e s = 0,5k g / m 3 ; A 1 =
Dados D 1 = 10c m ; ρ = 1000k g / m 3 ; H p 0,1 = 2,8m ; D 2 = 8c m ; H p 0 , e = 1,5m ; H p s , 2 = 2,4m ; η B = 0,7 . Calcular:a) a potência no eixo da bomba para que o corpo apoiado nas rodas sem a
Um jato atinge uma pá que se localiza num plano inclinado. O peso do conjunto é 40 N e a área do jato é 50 cm². Qual deverá ser a velocidade do jato para que o sistema permaneça em equilíbrio? ( γ = 1