Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 74

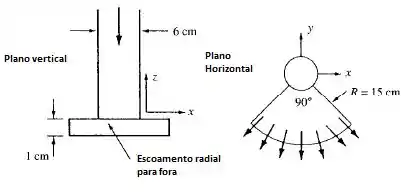
Água a 20°C escoa para baixo através de um tubo vertical de 6 cm de diâmetro, a 1136 L/min como na figura abaixo. O escoamento é então defletido horizontalmente e sai através de um segmento de duto radial de 1 cm de largura, como mostrado também na figura. Se o escoamento radial para fora é uniforme e permanente, calcule as forças Fx, Fy, Fz necessárias para suportar o sistema contra as variações de quantidade de movimento.

Passo 1

Primeiro de tudo vamos converter essa vazão aí pra unidade que a gente está acostumado, beleza?

Q ˙ = 1136 L m i n m 3 1000 L m i n 60 s = 0,01893   m 3

Ou seja, já de cara podemos calcular nossa vazão mássica sendo: m ˙ = Q ρ = 0,01893   x   998 = 18,9   k g / s

Passo 2

Agora vamos calcular a velocidade vertical pra baixo do tubo, show?

- V b a i x o = 0,01893 π 4 0,06 2 = - 6,7   m / s

Bem, a gente também sabe calcular qual é a área de saída do tubo: π 2 R Δ h

A s = π 2 0,15 0,01 = 0,002356   m 2

Portanto, a velocidade de saída pode ser encontrada facilmente, uma vez que conhecemos a vazão e sua área.

V s = Q A s = 0,01893 0,002356 = 8   m / s

Passo 3

Agora vamos partir pros balanços de forças em todas as componentes!!! LERIGOUUUUUUUUUUUU!!!!

∑ F X = F x = ∫ V s d m s ˙ = ∫ 0 90 ° - V s s e n θ ρ Δ h R d θ = 0

∑ F y = F y = ∫ V s d m ˙ s - m ˙ V e = ∫ - 45 ° 45 ° - V s c o s θ ρ Δ h R d θ - 0 = - V s ρ Δ h R 2

F y = - 8 998 0,01 0,15 2 = - 17   N

∑ F z = F z = m ˙ W s - W e = 18,9 0 - - 6,7 = 126   N

Resposta

F x = 0

F y = - 17   N

F z = 126   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o escoamento na redução de seção do tubo da figura abaixo, com D 1 = 8c m , D 2 = 5c m e p 2 = 1a t m . Todos os fluidos estão a 20°C. Se V 1 = 5m / s e a leitura do manômetro é de h = 58c m , ca
Um jato líquido com velocidade V j e área A j atinge uma única concha do rotor de uma turbina girando com velocidade angular Ω . Deduza uma expressão para a potência P fornecida pelo rotor nesse insta
Considere o escoamento incompressível na entrada de um tubo, como mostrado a seguir. O escoamento na entrada é uniforme, u 1 = U 0 . O escoamento na seção 2 já está desenvolvido. Encontre a força de a
Um tubo de 12 cm de diâmetro, contendo água escoamento a 200 N/s, sofre uma restrição por uma placa de orifício, como mostra a figura abaixo. O jato de saída tem 25 mm de diâmetro. A pressão no tubo n
Na figura abaixo, o jato atinge a pá movendo-se para a direita à velocidade constante V c em um carrinho sem atrito. Calcule (a) a força F x requerida para conter o carrinho e (b) a potência P entregu