Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 87

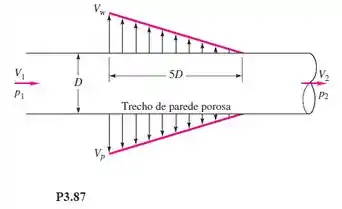
A Figura P3.87 simula um escoamento com múltiplas derivações, com o fluido sendo removido por uma parede porosa ou por um trecho perfurado do tubo. Admita escoamento incompressível com atrito desprezível na parede e pequena sucção, V p ≪ V 1 . Se ( p 1 , V 1 , V p , ρ ,   D ) são conhecidos, deduza expressões para (a) V 2 e (b) p 2 .

Passo 1

Simbora pra essa questão!

Cara, aqui nosso volume de controle vai ser da seção 1 até a 2, desconsiderando as paredes em si pois também vamos desconsiderar o atrito! Assumindo um escoamento incompressível, vamos utilizar a conservação de massa, assim:

V 1 A 1 = V 2 A 2 + ∫ 0 5 D V p 1 - x 5 D π D d x  

A integral é por conta do trecho de parede porosa, resolvendo-a:

V 1 π 4 D 2 = V 2 π 4 D 2 + 2,5 π V p D 2

Assumindo que, V p ≪ V 1 , teremos que:

V 2 = V 1 - 10 V p

Passo 2

Para (b), vamos utilizar uma relação de momento, assim:

∑ F x = p 1 - p 2 π 4 D 2 - ∫ τ p d A p = m ˙ 2 u 2 - m ˙ 1 u 1 + ∫ u p d m ˙ p

Considerando atrito desprezível e u p ≈ 0 , além de, A 1 cancelar a área de saída, teremos:

p 2 = p 1 + ρ V 1 2 - V 2 2

Substituindo a relação que encontramos para (a), temos:

p 2 = p 1 + 20 ρ V p ( V 1 - 5 V p )

Resposta

  1. V 2 = V 1 - 10 V p
  2. p 2 = p 1 + 20 ρ V p ( V 1 - 5 V p )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na instalação esquematizada na figura, (T) é uma turbina e o fluido que escoa é água de massa específica ρ = 1000k g / m 3 . A vazão que escoa é 314 L/s e as pressões em (1) e (2) são, respectivamente
O cotovelo da figura está preso por duas luvas elásticas para que não seja influenciado pelo resto da instalação. Sendo a área de sua seção 20 cm² e a vazão 20 L/s, qual será a força causada pelo esco
Sabendo que a perda de carga no trecho (1)-(2) é 3 m, determinar as componentes horizontal e vertical da força aplicada pelo fluido nesse trecho de tubulação. Dados: γ = 10000N / m 3 ; Q = 6L / s .
A turbina da figura ‘extrai’ a potência de 2,9 kW da água em escoamento. Desprezando as perdas na redução, calcular as forças exercidas pela água sobre a redução e sobre a turbina, respectivamente. Da
A água contida no tanque (1) é descarregada através do bocal sem atrito. Seu nível h 1 pode ser considerado constante. O jato incide sobre uma placa de grandes dimensões que cobre a saída do bocal do