Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 154
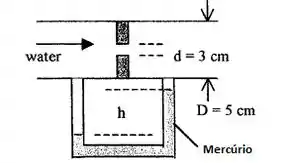
Água a 20°C escoa pelo orifício na figura abaixo, monitorado por um manômetro de mercúrio. Se d = 3cm, (a) qual é o valor de h quando a vazão é de 20 m³/h e (b) qual é o valor de Q em m³/h quando h = 58 cm?
Passo 1
E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?
Esse problema quer que a gente use bastante essa relação aqui de baixo!!!
Temos a vazão, a área de escoamento do orifício, mas onde vamos obter nosso bendito h que é pedido na letra (a)?
Passo 2
(a) A altura h está ali escondidinha dentro do nosso , porque ali dentro do tubo ele vai obedecer a hidrostática!
Além disso, o valor de
Mas ainda precisamos calcular o coeficiente de descarga, !!!!
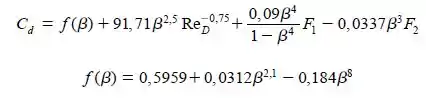
Onde para nosso caso pois podemos considerar tomadas em cantos, beleza?
Bem, então precisamos calcular nosso valor de Reynolds, como sendo:
Substituindo esses valores na nossa equação para o coeficiente de descarga, vamos obter que:
Passo 3
Substituindo na equação principal lá do nosso passo 1, vamos ter:
Passo 4
Resolvendo esse problema quando h = 58 cm é conhecido e Q é uma variável desconhecida...bem, é moleza né? Poque esse é exatamente o mesmo valor que encontramos na letra (a) quando temos
Ou seja, para h = 58 cm, temos que .