Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 160

É proposto resfriar com ar os cilindros de uma câmara de combustão através da fixação de um revestimento de alumínio com aletas anulares ( k   =   240   W / ( m   ·   K ) ) à parede do cilindro ( k   =   50   W / ( m   ·   K ) ) .

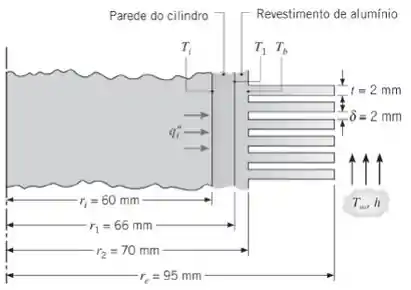
O ar está a 320   K e o coeficiente de transferência de calor correspondente é igual a 100   W / ( m 2   ·   K ) . Embora o aquecimento na superfície interna seja periódico, é razoável supor condições de regime estacionário com um fluxo térmico médio no tempo de q i ' ' =   10 5   W / m 2 . Considerando desprezível a resistência de contato entre a parede e o revestimento, determine a temperatura interna da parede T i , a temperatura na interface T 1 e a temperatura na base das aletas T b . Determine essas temperaturas se a resistência de contato na interface fosse de R t , c ' ' =   10 - 4   m 2   ·   K / W .

Passo 1

Bora para mais uma questão! Aqui nós temos as dimensões e os materiais de uma parede de cilindros aletada (anular). Além do fluxo de calor, condições do ar ambiente e o contato de resistência. Onde o circuito térmico é:

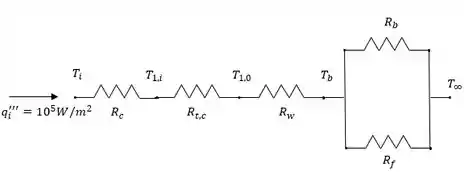
E queremos encontrar as temperaturas da superfície e da interface sem e com resistência de contato da interface.

Passo 2

Para resolver essa questão vamos assumir que:

(1) As condições são unidimensionais em estado estacionário;

(2) As propriedades são constantes;

(3) h é uniforme sobre as superfícies;

(4) A radiação é desprezível.

A análise pode ser realizada por unidade de comprimento do cilindro ou por uma seção de 4   m m de comprimento. Os cálculos a seguir são baseados no comprimento de uma unidade e a temperatura da superfície interna pode ser obtida por:

q ' = T i - T ∞ R t o t ' = q i ' ' 2 π r i = 10 5 W m 2 × 2 π × 0,06 m = 37700   W / m

Onde,

R t o t ' = R c ' + R t , c ' + R w ' + R e q u i v '

E,

R e q u i v ' = 1 R f ' + 1 R b ' - 1

Passo 3

R c ' é a resistência de condução da parede do cilindro e pode ser escrito como:

R c ' = ln ⁡ r 1 r i 2 π k = ln ⁡ 66 60 2 π 50 W m   ·   K = 3,034 × 10 - 4 m . K W

R t , c ' é a resistência de contato e pode ser escrito como:

R t , c ' = R t , c ' ' 2 π r 1 = 10 - 4     m 2 . K W 2 π × 0,066 m = 2,411 × 10 - 4 m . K W

R w ' é a resistência de condução da base de alumínio e pode ser escrito como:

R w ' = ln ⁡ r b r 1 2 π k = ln ⁡ 70 66 2 π 24 0 W m   ·   K = 3,902 × 10 - 5 m . K W

R b ' é a resistência da superfície principal ou não aletada e pode ser escrito como:

R b ' = 1 h A b ' = 1 100 W m 2   ·   K × 0,5 × 2 π ( 0,07 m ) = 454,7 × 10 - 4 m . K W

R f ' é a resistência das aletas e pode ser determinada por:

R f ' = T b - T ∞ q f ' = 1 f h A f '

Passo 4

A eficiência da aleta pode ser obtida por:

r 2 c = r o + t 2 = 0,096 m

L c = L + t 2 = 0,026 m

A p = L c t = 5,2 × 10 - 5 m 2

r 2 c r 1 = 1,45

L c 3 2 h k A p 1 2 = 0,375

Pela Fig. 3.20 temos que f ≈ 0,88 .

A área total da superfície da aleta por metro de comprimento é:

A f ' = 250 π r o 2 - r b 2 × 2 = 250 m - 1 2 π 0,096 2 - 0,07 2 m 2 = 6,78 m

Então,

R f ' = 0,88 × 100 W m 2 . K × 6,78 m - 1 = 16,8 × 10 - 4 m . K W

1 R e q u i v ' = 1 16,8 × 10 - 4 + 1 454,7 × 10 - 4 W m . K = 617,2 W m . K    

R e q u i v ' = 16,2 × 10 - 4 m . K W

Passo 5

Desprezando a resistência do contato, temos:

R t o t ' = 3,034 + 0,390 + 16,2 10 - 4 m . K W = 19,6 × 10 - 4 m . K W

T i = q ' R t o t ' + T ∞ = 37700 W m × 19,6 × 10 - 4 m . K W + 320 K = 393,9   K

T 1 = T i - q ' R w ' = 393,3   K - 37700 W m × 3,034 × 10 - 4 m . K W = 3 82,5   K

T b = T 1 - q ' R b ' = 3 82,5   K - 37700 W m × 3 , 902 × 10 - 5 m . K W = 38 1,0   K

Passo 6

Incluindo a resistência do contato, temos:

R t o t ' = 19,6 + 2,411 10 - 4 m . K W = 22,0 × 10 - 4 m . K W

T i = q ' R t o t ' + T ∞ = 37700 W m × 22,0 × 10 - 4 m . K W + 320 K = 402,9   K

T 1 , i = 402,9   K - 37700 W m × 3,034 × 10 - 4 m . K W = 391,5   K

T 1 , 0 = 391,5   K - 37700 W m × 2,411 × 10 - 5 m . K W = 382,5   K

T b = T 1 - q ' R b ' = 382 , 4   K - 37700 W m × 3,902 × 10 - 5 m . K W = 38 0 , 9   K

Resposta

Desprezando a resistência do contato:

T i = 393,9   K

T 1 = 382,5   K

T b = 381,0   K

Incluindo a resistência do contato:

T i = 402,9   K

T 1 , i = 391,5   K

T 1,0 = 382 , 4   K

T b = 380,9   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na medida em que mais e mais componentes são colocados em um único circuito integrado (chip), a quantidade de calor dissipada também aumenta. Entretanto, esse aumento está limitado pela máxima tempera
Como um meio para aumentar a transferência de calor em circuitos integrados (chip) lógicos de alto desempenho, é comum a fixação de um dissipador de calor à superfície do chip, com o objetivo de aumen
Um chip de silício isotérmico, com um lado de comprimento W=20m m , encontra-se soldado a um dissipador de calor de alumínio ( k=180W / ( m·K ) ) com comprimento equivalente. O dissipador tem uma base
Uma aleta anular de alumínio com perfil retangular está fixada a um tubo circular que possui um diâmetro externo de 25m m e uma temperatura superficial de 250 ° C . A aleta possui 1m m de espessura e