Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 125
Água deve escoar por gravidade de um reservatório para outro mais baixo através de um tubo de aço galvanizado, retilíneo e inclinado. O diâmetro do tubo é 50 mm e o comprimento total é de 250 m. Os dois reservatórios estão abertos para atmosfera. Trace um gráfico da diferença de elevação requerida Δz como uma função da vazão Q, para Q variando de 0 a 0,01 m3/s. Estime a fração de Δz decorrente de perdas menores.
Passo 1
Oi pessoal, tudo bem ?
Bem, para encontrar a faixa de valores para a elevação requerida entre os reservatórios, deve-se lembrar primeiramente da equação da energia:
Passo 2
Considerações a serem feitas::
Considerando o tanque muito grande, considera-se a velocidade nula,
A profundidade pode ser analisada como
Segundo o autor, a perda de carga é dada pela soma da perda de carga menor com a menor, então:
Reescrevendo a equação da perda de carga:
O fator de atrito pode ser dado de duas formas diferentes:
), quando o escoamento for turbulento;
, quando o escoamento for laminar.
E o número de Reynolds (Re) é dado pela expressão:
Por sua vez, a relação entre a vazão e a velocidade é:
Passo 3
Então, como todas as expressões interdependem entre si, ao variar os valores das vazões no reservatório, haverá uma variação em cadeia: primeiro da velocidade, depois do Re, depois do coeficiente de atrito, até a profundidade do tanque.
Valores a serem considerados:
| | (escoamento turbulento) | | | |
(Tabela 8.2) e supondo a rugosidade (Tabela 8.1)
Resposta
Colocando os valores ordenados no Excel com suas respectivas fórmulas, e utilizando a ferramenta Solve, é possível encontrar a variação de velocidades e os números de Reynolds correspondentes em relação à variação de vazão, como mostra a tabela a seguir:
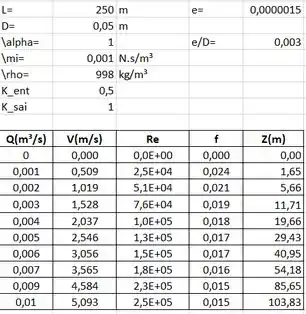
O valor de f é proveniente de:
), pois o escoamento é turbulento (Re>2300);
Assim, o gráfico da variação da vazão versus a variação da profundidade fica:
