Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 55
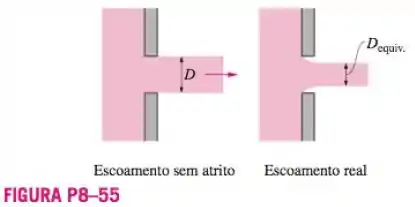
Considere o escoamento de um reservatório de água através de um orifício circular de diâmetro na parede lateral a uma distância vertical da superfície livre. A vazão através de um orifício real com uma entrada em aresta viva será consideravelmente menor do que a vazão calculada considerando escoamento “sem atrito” e, portanto, perda zero no orifício. Desprezando o efeito do fator de correção da energia cinética, obtenha uma relação para o “diâmetro equivalente” do orifício com aresta viva para uso nas relações de escoamento sem atrito.
Passo 1
Temos que determinara relação do , para isto, podemos utilizar a relação de que com atrito ou sem atrito a vazão volumétrica será a mesma. Devido a isto, teremos a nossa relação.
Assumindo que o fluxo é constante e incompressível, o reservatório é aberto para atmosfera e o fator de correção de energia cinética será .
Escolhendo dois pontos de nível, temos:
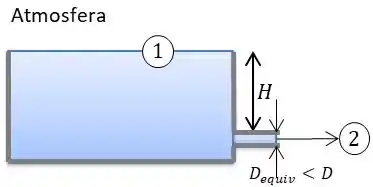
Ponto 1 está na superfície livre da água, ponto 2 na superfície libre da água ao sair do tanque e tomaremos o ponto 2 como .
Como os dois pontos estão abertos para atmosfera teremos .
E a velocidade no ponto 1 será aproximadamente zero, como não conhecemos as dimensões do tanque, com um tanque muito grande a velocidade de esvaziamento é muito pequena, a velocidade tende .
Passo 2
Seguindo a lógica e fatos no passo 1, temos que determinara velocidade de saída para trabalhar com a vazão volumétrica.
Podemos determinar a velocidade de saída pela equação do balanço energético.
Simplificando a equação, temos:
Nesta equação, nós falta determinar .
Passo 3
Temos que é definido por:
Substituindo na equação do balanço:
Simplificando a equação e isolando :
Passo 4
Temos a equação da velocidade, vamos determinara vazão:
Como enunciado pede para trabalharmos com e , portanto:
Para :
Substituindo valores:
Para :
Substituindo valores:
Passo 5
Determinamos às duas vazões com seus respectivos fatores de perda, partiu determinar a relação :
Igualando as equações (1) e (2), temos:
Simplificando:
Elevando os dois lados ao quadrado:
E isolando :