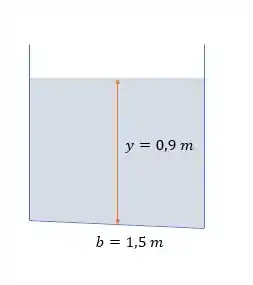
Água escoa através de um canal retangular com 1,5 m de largura com um coeficiente de Manning de n = 0,012. Se a profundidade da água for 0,9 m e a inclinação do fundo do canal

for 0,6°, determine a taxa de descarga do canal no escoamento uniforme.

Começando pela área transversal, :

O rai hidráulico é calculado por:

O perimetro molhado, por sua vez é:

Logo :

E por fim a gente calcula que é dado pela tangente da inclinação do canal:

Agora é só substituir e correr pro abraço:

Calculando:

Aweee!