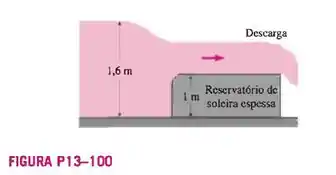
Um reservatório de soleira espessa com 1 m de altura é usado para medir a vazão da água em um canal retangular com 5 m de largura. A profundidade de escoamento bem a montante do reservatório é de 1,6 m. Determine a vazão através do canal e a profundidade de escoamento mínima acima do reservatório.
Passo 1
Bora lá pra mais uma questão!!
A gente quer descobrir a vazão do canal e a profundidade mínima do escoamento acima do reservatório, , como podemos ver na figura:

Podemos calcular a vazão usando essa formulinha aqui:
A largura dada no enunciado é e calculando a carga do reservatório, :
Só falta conhecermos o coeficiente de descarga, !
Passo 2
Para calcular usamos:
Substituindo os valores:
Podemos então substituir os dados para calcular a vazão:
Calculando:
Passo 3
Agora queremos achar o a profundidade mínima, e isso acontece no ponto crítico, quando , então:
Podemos substituir e calcular:
Aweee!!!