Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 112

13-112 Água escoa em um canal cuja inclinação do fundo é de 0,5 ° e cuja seção transversal é aquela mostrada na Figura P13-126. As dimensões e os coeficientes de Manning para as

superfícies de diferentes subseções também são dadas na figura. Determine a vazão de escoamento através do canal e o coeficiente de Manning efetivo do canal.

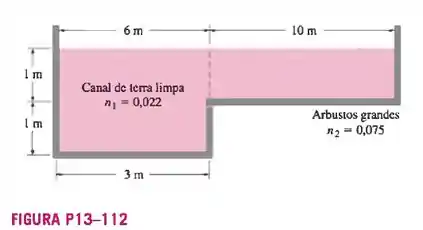
Passo 1

Bora fazer mais uma questão!!

E o que temos aqui?!

Um canal com duas subsecções diferentes e queremos achar a vazão do escoamento o coeficiente de Manning efetivo do canal!

A vazão pode ser calculada por:

V ˙ = a n A R 2 3 S 0 1 2

Mas como temos duas partes do canal, com rugosidades diferentes então vamos dividir as áreas e somar as vazões:

V ˙ = V 1 ˙ + V 2 ˙

Temos um esqueminha que mostra quem é A 1 e quem é A 2 :

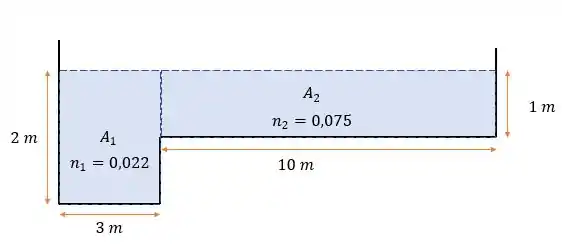
Então para calcular a vazão total ficamos com:

V ˙ = a n 1 A 1 R 1 2 3 S 0 1 2 + a n 2 A 2 R 2 2 3 S 0 1 2

Passo 2

Vamos calcular as áreas e os raios hidráulicos para podemos calcular a vazão!

A 1 = 3 × 2 = 6   m 2

A 2 = 10 × 1 = 10 m 2

O raio hidráulico é dado por:

R h = A p

Então temos:

R h 1 = 6 2 + 3 + 1 = 1   m

R h 1 = 10 10 + 1 + 1 = 0,909   m

Passo 3

Lembrando que a = 1 m 1 3 / s e S 0 é a tangente da inclinação 0,5 ° , então podemos calcular V ˙ :

V ˙ =   1 0,022 × 6 × 1 2 3 × tan ⁡ 0,5 ° 1 / 2   +   1 0,0 75 × 10 × 0,909 2 3 × tan ⁡ 0,5 ° 1 / 2  

Jogando tudo na calculadora:

V ˙ = 37,2   m 3 / s

Passo 4

Agora que a gente conhece a vazão, podemos calcular o n e f f isolando o n na equação de Manning, quando fazemos isso ficamos com:

n e f f = a A c R h 2 3 S 0 1 2 V ˙

A área aqui é total, dada pela soma das áreas:

A c = 6 + 10 = 16 m 2

E o raio hidráulico pode ser calculado:

R h = A c p = 16 2 + 3 + 10 + 1 = 0,941   m

Podemos substituir:

n e f f = 1 × 16 × 0,941 2 3 × tan ⁡ 0,5 ° 1 / 2   37,2

E achamos:

n e f f = 0,0386

Uhuuuul!!!

Resposta

V ˙ = 37,2   m 3 / s

n e f f = 0,0386

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

What are the most effi cient dimensions for a half-hexagoncast iron channel to carry 15,000 gal/min on a slopeof 0.168?
A rectangular channel, laid out on a 0.58 slope, delivers aflow rate of 5000 gal/min in uniform fl ow when the depthis 1 ft and the width is 3 ft. (a) Estimate the value ofManning’s factor n. (b) What
A V-shaped painted steel channel, similar to Fig. E10.6,has an included angle of 908. If the slope, in uniform flow,is 3 m per km, estimate (a) the fl ow rate, in m3/s and (b) theaverage wall shear st
A new, finished-concrete trapezoidal channel, similar toFig. 10.7, has b 5 8 ft, yn 5 5 ft, and θ 5 508. For thisdepth, the discharge is 500 ft3/s. (a) What is the slope of thechannel? (b) As years pa
A circular corrugated-metal water channel has a slope of1:800 and a diameter of 6 ft. (a) Estimate the normal discharge, in gal/min, when the water depth is 4 ft. (b) For thiscondition, calculate the