Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 122

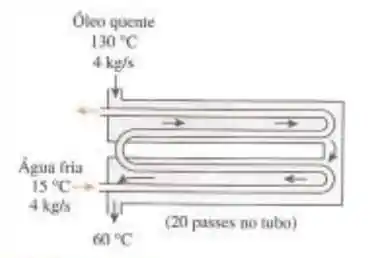
Água fria c p = 4180 J k g K entra nos tubos de um trocador de calor com 2 passes no casco e 20 passes no tubo a 15°C, a uma taxa de 4 k g s , enquanto óleo quente c p = 220 0 J k g K entra no casco a 130°C com a mesma vazão mássica e sai a 60°C. Considerando que o coeficiente global de transferência de calor com base na superfície externa do tubo é 220 W m 2 K , determine (a) a taxa de transferência de calor e (b) a superfície de transferência de calor na face externa do tubo.

Passo 1

Beleza galerinha, vamos achar a taxa de transferência de calor, ok?

Usando a transferencia de calor doada pelo óleo quente:

Q ˙ = m o l e o ˙ c p ,   o l e o ( T o l e o ,   e n t r a - T o l e o ,   s a i )

Nós sabemos que:

m o l e o ˙ = 4 k g s

c p ,   o l e o = 220 0 J k g K

T o l e o ,   e n t r a = 130 ° C

T o l e o ,   s a i = 60 ° C

Olha que legal !!!

Já achamos tudo o que precisamos, certo?

Agora é só achar o calor:

Q ˙ = 4 k g s 220 0 J k g K ( 130 ° C - 6 0 ° C )

Q ˙ = 616000   W

Ou melhor:

Q ˙ = 616   k W

Já achamos a resposta da letra (a), agora só precisamos achar a da letra (b) !!

Passo 2

O nosso próximo passo é calcular a área superficial de transferência de calor na face externa do tubo, ok?

Para isso podemos usar a equação:

Q ˙ = U F A s ∆ T l m

Isolando:

A s = Q ˙ U F ∆ T l m

Já sabemos que:

U = 2 2 0 W m 2 K = 0 , 22 k W m 2 K

Q ˙ = 616   k W

Mas nada sobre F e ∆ T l m , certo?

Começando pela diferença média logarítima:

∆ T l m = ∆ T 1 - ∆ T 2 ln ⁡ ∆ T 1 ∆ T 2

Se:

∆ T 1 = T q ,   e n t r a - T f ,   s a i

∆ T 2 = T q ,   s a i - T f ,   e n t r a

Lembrando que:

T q ,   e n t r a = 13 0 ° C

T q ,   s a i = 6 0 ° C

T f ,   e n t r a = 15 ° C

Complicoou !! Não sabemos nada sobre a temperatura de saída da água, mas vamos acha-la rapidinho usando a fórmula:

Q ˙ = m f ˙ c p , f ( T f ,   s a i - T f ,   e n t r a )

Se:

m f ˙ = 4 k g s

c p , f = 4 , 18 k J k g K

Então:

616   k W = 4 k g s 4 , 18 k J k g K ( T f ,   s a i - 15 ° C )

T f ,   s a i = 51,84 ° C

Agoora sim nós podemos calcular a diferença de temperatura média logarítima:

∆ T 1 = 13 0 ° C - 51,84 ° C = 78,16 ° C

∆ T 2 = 6 0 ° C - 15 ° C = 45 ° C

Substituindo:

∆ T l m = 78,16 ° C - 45 ° C ln ⁡ 78,16 ° C 45 ° C

∆ T l m = 60,062 ° C

Passo 3

Para o fator de correção, F, vamos precisar olhar a figura:

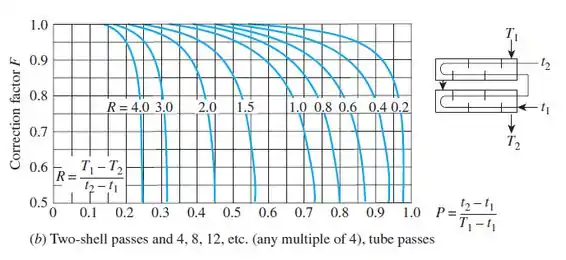
Vamos começar calculando R e P:

R = T q ,   e n t r a - T q ,   s a i T f ,   s a i - T f ,   e n t r a = 13 0 ° C - 6 0 ° C 51,84 ° C - 15 ° C = 1,9

P = T f ,   s a i - T f ,   e n t r a T q ,   e n t r a - T f ,   e n t r a = 51,84 ° C - 15 ° C 13 0 ° C - 15 ° C = 0 , 32

Então:

F ≅ 0,9 7

Agoora siiim !!

Vamos colocar tudo isso na fórmula da área da superfície:

616   k W = 0,2 2 k W m 2 K 0,9 7 A s 60,062 ° C

A s = 48   m ²

Gostaram dessa, né?!

Resposta

  1. Q ˙ = 616   k W ;
  2. A s = 48   m ² .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51 - Reconsidere Prob.11-50.Usando EES (ou outro programa), investigue o efeito da vazão de mássica da água sobre a taxa de transferência de calor e a superfície no lado do tubo.Deixe a vazão mássica
50 - Um trocador de calor de casco e tubo com 2 passes no casco e 12 passes no tubo é utilizado para aquecer água c p = 4180 J k g ⋅ K com etilenoglicol c p = 2680 J k g ⋅ K .A água entra no tubo a 22
39 - Um trocador de calor de fluxo cruzado de único passe é utilizado para resfriar a água ( c p = 4,18k J / k g ⋅ ℃ ℃) de um motor a diesel de 90℃ ℃ para 60℃ ℃, usando ar ( c p = 1,02k J / k g ⋅ ℃ )
Um trocador de calor bitubular (tubos concêntricos) em contracorrente é projetado para aquecer água de 20 a 80°C, utilizando óleo quente, que é alimentado na região anular a 160°C e retirado a 140°C.
Um radiador de automóvel pode ser visto como um trocador de calor com escoamento cruzado, com os dois fluidos não misturados. Água, a uma vazão de 0,05k g / s , entra no radiador a 400K e deve deixá-l