A água em uma piscina acima do solo a , com de diâmetro e de altura deve ser esvaziada destampando um tubo plástico horizontal com de diâmetro e de comprimento anexado à parte inferior da piscina. Determine taxa inicial de descarga da água através do tubo e o tempo necessário para esvaziar a piscina completamente, considerando que a entrada do tubo seja bem arredondada, com perda desprezível. Tome o fator de atrito do tubo como . Usando a velocidade de descarga inicial, verifique se esse é um valor razoável para o fator de atrito.
Passo 1
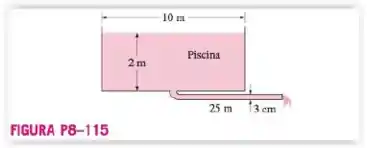
Bom, gente, aqui nesse problema nós temos uma piscina e um tubo conectados, assim devemos encontrar a taxa inicial de descarga da água através do tubo e o tempo necessário para esvaziar a piscina completamente.
Fiquemos atentos a temperatura dada, para ela temos: , , a rugosidade na tubulação e o fator de atrito é .
O efeito do fator de correção da energia cinética não faz muita diferença, então .
Passo 2
Desprezando as perdas menores, podemos utilizar a equação de energia (que é a de Bernoulli, com alguns acréscimos). Assim, estabelecendo os pontos de análise e , temos:
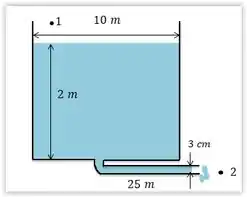
Pelo diagrama, os pontos e são expostos a atmosfera, ou seja, . Além disso, o nosso ponto de referência é em e a velocidade no ponto é desprezível, ou seja, . Por ultimo, não temos bomba nem turbina, então e . Assim, temos:
Como , então:
Isolamos a velocidade de saída:
Calculando, temos:
Assim, podemos calcular a vazão de descarga:
Passo 3
Para acharmos o tempo que a piscina esvazia completamente, podemos expressar a quantidade de água saindo durante um instante de tempo através da derivação:
Sendo que , logo
A massa que sai é igual a que está dentro do tanque, pelo fato de esvaziar, ocorre uma diminuição de nível:
Igualando as expressões e substituindo as variáveis, temos:
Isolando :
Passo 4
Vamos resolver nossa integral. Para isso, vale lembrar que o intervalo de tempo é e a altura , logo:
Substituindo os dados, temos:
Prontinho!!
Resposta
e