Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 73
Água pressurizada a Tm,ent = 200°C é bombeada a uma vazão de = 2 kg/s de uma planta de potência para um usuário industrial próximo, através de um tubo circular de parede delgada e com diâmetro interno D = 1 m. O tubo é revestido por uma camada de isolamento térmico com espessura t = 0,15 m e condutividade térmica k = 0,05 W/(m · K). O tubo, que tem um comprimento L = 500 m, está exposto a um escoamento cruzado de ar a T∞ = –10°C e V = 4 m/s. Obtenha uma equação diferencial que possa ser usada para determinar a variação da temperatura média da água Tm(x) em função da coordenada axial. Como uma primeira aproximação, o escoamento interno pode ser considerado plenamente desenvolvido ao longo de todo o tubo. Expresse os seus resultados em termos de , V, T∞, D, t, k e das propriedades apropriadas da água (a) e do ar (ar). Calcule a perda de calor por unidade de comprimento na entrada do tubo. Qual é a temperatura média da água na saída do tubo?
Passo 1
Beleza galerinha, vamos lá! (a) Seguindo o desenvolvimento da Secção 8.3.1 e aplicando Eq. 1.12e a um elemento diferencial na água, obtemos,
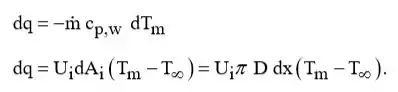
Substituindo no balanço energético, segue-se que,
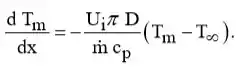
Passo 2
O coeficiente global de transferência de calor com base na área de superfície interna pode ser avaliado a partir da Eq. 3.36 que, para as condições atuais, reduz para
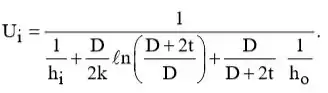
Para o fluxo interno de água, Eq. 8.6 dá,
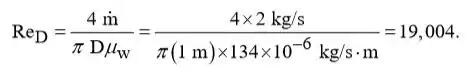
Portanto, o fluxo é turbulento. Com a suposição de condições totalmente desenvolvidas, decorre da Eq. 8.60 que,
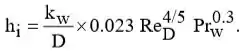
Para o fluxo de ar externo,
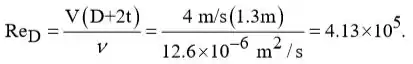
Usando Eq. 7,53 para obter o coeficiente de convecção externa,
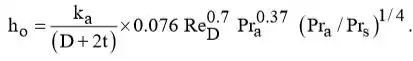
Passo 3
(b) A transferência de calor por unidade de comprimento de tubo na entrada é,
Das eqs anteriores:
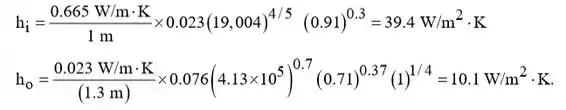
Logo,
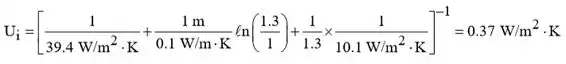
Portanto,
