Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 7.Problemas - Ex. 56
Agua quente a 50°C é transportada de um prédio no qual ela é gerada para um prédio adjacente no qual ela é usada para aquecimento ambiental. A transferência entre os prédios ocorre em tubo de aço ( k — 60 W/(m- K)), com diâmetro externo de 100 mm e 8 mm de espessura de parede. Durante o inverno, condições ambientais representativas envolvem o ar a T„- —5°C e V = 3 m/s em escoamento cruzado sobre o tubo. (a) Se o custo de produzir a água quente é de $0,05 por kW h, qual é o custo diário representativo da perda térmica para o ar em um tubo não isolado, por metro de comprimento de tubo? A resistência convectiva associada ao escoamento da água no interior do tubo pode ser desprezada. (b) Determine a economia associada à aplicação na superfície externa do tubo de um revestimento de 10 mm de espessura de isolante de uretano ( k — 0,026 W/(m K)
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Temos que com
Assim conseguimos aplicar a correlação de Churchill-Bernstein, da seguinte forma:
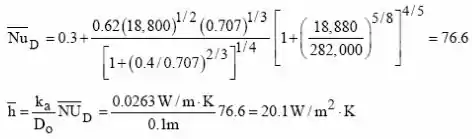
Sem o isolamento, a resistência térmica total e a perda de calor por polegada de tubo são:
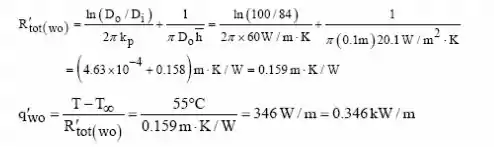
Correspondendo a uma perda de energia diária de:
E que se for associado ao custo:
Passo 2
Aqui no item b), a resistência de condução do isolamento pode ser dado por:
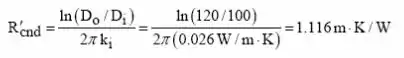
Usando a correlação de Churchill-Bernstein, temos que a resistência de convecção é:
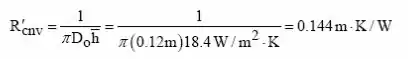
E a resistência total:
Assim calculando a perda de calor e os custos:
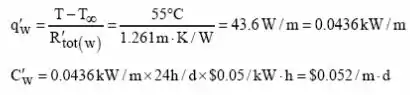
Portanto a economia diária é dada pela diferença entre os dois:
