Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 1
Um gás ideal a 20°C e 1 atm escoa a 12 m/s sobre uma placa plana fina. Em uma posição 60 cm a jusante do bordo de ataque, a espessura da camada-limite é de 5 mm. Dos 13 gases da Tabela A.4, qual é o provável gás em questão?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos um gás ideal não identificado escoando a e com uma velocidade em uma placa fina.
De acordo com o enunciado, a uma posição de da borda de ataque, temos uma espessura de camada limite igual .
Com esses dados, deveremos calcular a viscosidade cinemática do gás para essas condições. Pra isso, devemos lembrar as equações da camada limite para uma placa plana são:
Nos próximos passos nós vamos calcular e descobrir qual gás é esse que a gente ainda não sabe.
Vem comigo pra gente resolver essa questão juntos!
Passo 2
Em primeiro lugar, como não podemos calcular o número de Reynolds, que depende da viscosidade cinemática, devemos assumir um regime de escoamento.
Vamos assumir o escoamento como laminar, mas depois a gente vai conferir se estamos certos em fazer isso.
Dessa maneira, a equação se torna:
Agora, pra confirmar se realmente estamos em um escoamento laminar, vamo calcular Reynolds:
Que está dentro da faixa , ou seja, acertamos na nossa suposição.
Passo 3
Agora, pra finalizar a questão, vamo descobrir qual o gás que está escoando.
Pra isso, vamos na Tabela A.4, intitulada “Propriedades dos gases comuns a 1 atm e 20°C”, na página 829.
Como demonstrado nesse esquema abaixo, a gente entra com o valor de viscosidade cinemática :
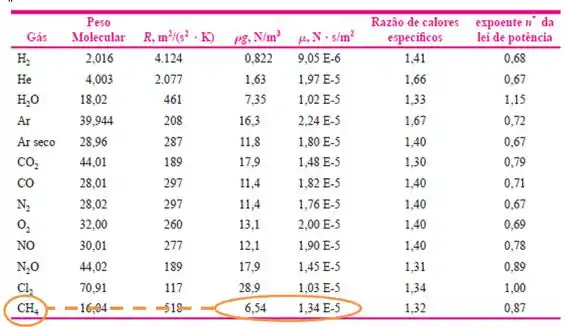
Se a gente dividir encontrados na tabela para o metano teremos .
Ou seja, o metano é o gás escoando nesse problema.
Pronto, matamos a questão juntos!
Resposta
O gás escoando nas condições deste problema é o metano ()