Um reator de gases de alta temperatura (HTRG -high-temperature gas reactor) possui elementos combustíveis à base de óxido de urânio de formato esférico, nos quais há aquecimento volumétrico uniforme ( q). Cada elemento combustível encontra-se revestido por uma casca esférica de grafite, que é resfriada pelo escoamento de gás hélio a 1 atm.

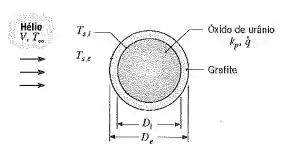
Considere condições de regime estacionário nas quais os efeitos radiantes podem ser desprezados, a velocidade e temperatura do gás são de V = 20 m/s e T„= 500 K, os diâmetros da partícula e da casca são de D, — 10 mm cD,= 12 mm, e a temperatura da superfície externa da casca é de Tse — 1300 K. O óxido de urânio e o grafite possuem condutividade térmica kp = kg = 2 W/(m-K). (a) Qual é a taxa de transferência de calor para a comente de gás a partir de uma única partícula?

(b) Qual é a taxa volumétrica de geração térmica na partícula e qual é a temperatura na interface entre a partícula e o grafite (r5 ,)? (c) Obtenha uma expressão para a distribuição radial de temperaturas, T(r), na partícula, apresentando o seu resultado em termos da temperatura no centro da partícula, 7' (0).Calcule 7’ (0) para as condições especificadas. |(d)|Determine T,e , Ts, e 7 ' {0) como uma função da velocidade do gás para 5 V 20 m/s e q = 1,50 X 10s W/m3 .

Para calcular a taxa de calor volumétrico, podemos achar através de:

A superfície de temperatura da cobertura é igual a temperatura de superfície do pallet,

No item c), temos que a equação de calor para um objeto esférico dado por:

Integrando duas vezes:

Aplicando as condições iniciais, temos que a distribuição de temperatura é dada por:

Desenvolvendo: