Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 136

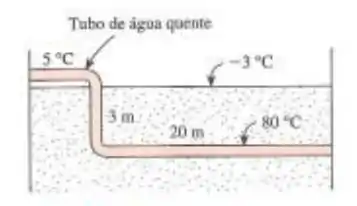
Água quente a uma temperatura média de 80°C e a uma velocidade média de 1,5 m/s flui através da seção de 25 m de um tubo que tem diâmetro externo de 5 cm. O tubo se estende por 2 m no ar ambiente acima do solo, penetra no solo k = 1,5 W m   ·   K   verticalmente por 3 m e continua horizontalmente nessa profundidade por mais 20 m, antes de entrar no próximo edifício. A primeira seção do tubo é exposta ao ar ambiente a 5°C, com um coeficiente de transferência de calor de 22 W m 2   ·   K . Considerando que a superfície do solo está coberta de neve a -3°C, determine:

  1. A taxa de transferência de calor a partir da água quente;
  2. A queda de temperatura da água quente ao percorrer essa seção de 25 m do tubo.

Passo 1

Bora pra mais uma, galerinha??

Aqui nós temos uma situação um pouco diferente das anteriores, concordam?

Nós temos o tubo trocando calor com o ambiente em três situações distintas, a primeira ele esta exposto ao ar, nas duas formas seguintes temos ele enterrado no solo, porém com duas configurações diferentes, vertical e horizontal:

Q T o t a l ˙ = Q 1 ˙ + Q 2 ˙ + Q 3 ˙

Vamos começar pelo Q 1 ˙ , ou seja, troca de calor convectivo com o ar ambiente.

Se lembram de como calculamos?

Q 1 ˙ = h A s T t u b o - T a r

Já temos que:

h = 22 W m 2   ·   K

T t u b o = 80 ° C

T a r = 5 ° C

A área da superfície do tubo é dada por:

A s = π D L 1

Se:

D = 5   c m = 0,05   m

L 1 = 2   m

Então:

A s = π 0,05   m 2   m = 0,31416   m 2

Agora que temos tudo basta calcularmos a toca de calor:

Q 1 ˙ = 22 W m 2   ·   K 0,31416   m 2 80 ° C - 5 ° C

Q 1 ˙ = 518,364   W

Passo 2

Já achamos o calor trocado pela primeira seção, certo?

Agora vamos achar o da segunda seção, onde o tubo está inserido verticalmente no solo.

Já sabemos que nesta situação podemos calculá-lo como:

Q 2 ˙ = S 2 k T t u b o - T s o l o

Já sabemos que:

k = 1,5 W m   ·   K

T t u b o = 80 ° C

T p a r e d e = - 3 ° C

Agora só precisamos calcular o S, o fator de forma de condução.

E como vamos calcula-lo?

Vamos olhar a geometria, certo?

Considerando um cilindro isotérmico circular de comprimento L enterrado verticalmente em um meio semi-infinito, nós podemos usar a fórmula:

S 2 = 2 π L 2 ln ⁡ 4 L 2 D

Se:

L 2 = 3   m

D = 5   c m = 0,05   m

Então:

S 2 = 2 π ( 3   m ) ln ⁡ 4 × 3   m 0,05   m = 3,44   m

Na fórmula do calor:

Q 2 ˙ = 3,44   m 1 , 5 W m   ·   K 80 ° C - ( - 3 ° C )

Q 2 ˙ = 428,28   W

Passo 3

Na seção 3 nós teremos o mesmo caso que o anterior:

Q 3 ˙ = S 3 k T t u b o - T s o l o

JÁ única coisa que varia aqui é o S!

Considerando um cilindro isotérmico circular de comprimento L enterrado horizontalmente em um meio semi-infinito, nós podemos usar a fórmula:

S 3 = 2 π L 3 ln ⁡ 4 z D

Onde z é a profundidade!

Se:

L 3 = 20   m

z = 3   m

Então:

S 3 = 2 π ( 20   m ) ln ⁡ 4 × 3   m 0,05   m = 22,93   m

Na fórmula do calor:

Q 3 ˙ = 22,93   m 1,5 W m   ·   K 80 ° C - ( - 3 ° C )

Q 3 ˙ = 2854,785   W

Agora sim !! Bora achar o calor total?

Q T o t a l ˙ = 518,364   W + 428,28   W + 2854,785   W

Q T o t a l ˙ = 3801,429   W

Passo 4

Achamos o calor trocado, mas ainda precisamos da resposta para a letra (b), não é?

Para achar a queda de temperatura da água quente à medida escoa por esses 25 m de comprimento nós podemos usar outra equação bastante conhecida:

Q T o t a l ˙ = m ˙ c p ∆ T

Isolando a variação da temperatura:

∆ T = Q T o t a l ˙ m ˙ c p

Sabendo que:

c p = 4180 J k g   ° C

E que o fluxo de massa é dado por:

m ˙ = ρ V A c

Se a seção transversal é circular:

m ˙ = ρ V π D 2 4

Substituindo nossos dados:

m ˙ = 1000 k g m 3 1,5 m s π ( 0,05   m ) 2 4 = 2,9452 k g s

Agora é só colocar na fórmula da variação da temperatura:

∆ T = 3801,429   W 2,9452 k g s 4180 J k g   ° C = 0 , 3087 ° C

Então a água que estará passando pelo tubo cai apenas 0,3087 ° C .

Gostaram?

Resposta

  1. 3801,429   W ;
  2. 0,3087 ° C .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja o Problema 4.5, agora com a placa tendo seção transversal quadrada, W = L . a) Deduza uma expressão para o fator de forma, S m á x á , associado à temperatura m á x i m a á na superfície superior
Uma placa retangular bidimensional está sujeita às condições de contorno especificadas. Usando os resultados da solução exata para a equação do calor apresentados na Seção 4.2, calcule a temperatura n
No método da separação de variáveis (Seção 4.2) para a condução bidimensional em regime estacionário, a constante de separação λ 2 nas Equações 4.6 e 4.7 deve ser uma constante positiva. Mostre que va
Uma placa retangular bidimensional está sujeita às condições de contorno mostradas na figura. Deduza uma expressão para a distribuição de temperaturas em regime estacionário T ( x , y ) .
Uma placa retangular bidimensional é submetida a condições de contorno de temperatura especificada em três lados e a condição de fluxo térmico uniforme para dentro da placa em sua superfície superior.