Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 04

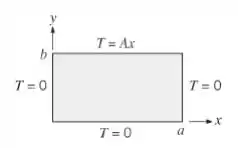
Uma placa retangular bidimensional está sujeita às condições de contorno mostradas na figura. Deduza uma expressão para a distribuição de temperaturas em regime estacionário T ( x , y ) .

Passo 1

Fala aí! Olha só, nessa questão precisamos deduzir a equação de temperatura nas condições mostradas, vamos lá!

Vamos começar com o seguinte:

T x ,   y = X ( x )   .   Y ( y )

T x ,   y = C 1 . c o s λ . x + C 2 . s e n λ . x   .   C 3 . e - λ . y + C 4 . e λ . y

E vamos definir nossas condições de contorno como sendo:

T ( 0 ,   y ) = 0 T ( a ,   y ) = 0

T ( x ,   0 ) = 0 T ( x ,   b ) = A   .   x

Agora podemos aplicar nossas condições de contorno para achar os valores das nossas constantes:

T 0 ,   y = C 1 . c o s λ . 0 + C 2 . s e n λ . 0   .   C 3 . e - λ . y + C 4 . e λ . y = 0

C 1 . c o s 0 + C 2 . s e n 0   .   C 3 . e - λ . y + C 4 . e λ . y = 0

C 1   .   C 3 . e - λ . y + C 4 . e λ . y = 0

C 1 = 0

Agora a segunda condição:

T a ,   y = C 1 . c o s λ . x + C 2 . s e n λ . x   .   C 3 . e - λ . y + C 4 . e λ . y = 0

T a ,   y = 0 . c o s λ . a + C 2 . s e n λ . a   .   C 3 . e - λ . y + C 4 . e λ . y = 0

C 2 . s e n λ . a   .   C 3 . e - λ . y + C 4 . e λ . y = 0

λ = n   .   π a

E nossa terceira condição nos dá que:

T x ,   0 = C 1 . c o s λ . x + C 2 . s e n λ . x   .   C 3 . e - λ . 0 + C 4 . e λ . 0 = 0

0 . c o s λ . x + C 2 . s e n λ . x   .   C 3 . e - 0 + C 4 . e 0 = 0

C 2   .   s e n λ . x   .   C 3 + C 4 = 0

C 3 =   - C 4

Nossa equação então vai ficar com essa carinha aqui, olha só:

T x ,   y = C 2 . s e n n . π a x   .   - C 4 . e - λ . y + C 4 . e λ . y

T x ,   y = C 2   .   C 4   .   s e n n . π a x   .   e λ . y - e - λ . y

Passo 2

Vamos ter o seguinte:

T x ,   y = ∑ n = 1 ∞ C n   .   s e n n . π . x a   .   s e n h n . π . x a

Vamos então verificar nosso C n , beleza?

C n = ∫ 0 a A   .   x   .   s e n n . π . x a . d x s e n h n . π . b a ∫ 0 a s e n ² n . π . x a . d x

E usando nossa última condição de contorno, em que y = 0 :

A   .   ∫ 0 a x . s e n n . π . b a .   d x   =   A   . a n . π 2 .   s e n n . π . x a - a . x n . π .   c o s n . π . x a | 0 a = A . a ² n . π . - c o s ( n . π ) = A . a ² n . π . - 1 n + 1  

s e n h n . π . b a .   ∫ 0 a s e n ² n . π . x a .   d x = s e n h n . π . b a . 1 2 x - a 4 . n . π .   s e n 2 . n . π . x a | 0 a = a 2   .   s e n h n . π . b a

Vamos ter então que:

C n = A . a ² n . π . - 1 n + 1 a / 2   .   s e n h n . π . b a

C n = 2 . A . a . - 1 n + 1 n   .   π   .   s e n h n . π . b a

Se encontramos o C n , nossa temperatura então será:

T x ,   y = 2 . A . a π   .   ∑ n = 1 ∞ - 1 n + 1 n   .   s e n n . π . x a   .   s e n h n . π . y a s e n h n . π . b a

Uhull!! Conseguimos!

Resposta

T x ,   y = 2 . A . a π   .   ∑ n = 1 ∞ - 1 n + 1 n   .   s e n n . π . x a   .   s e n h n . π . y a s e n h n . π . b a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto bidimensional é submetido a condições isotérmicas nas suas superfícies esquerda e direita, como mostrado no esquema. As duas superfícies diagonais são adiabáticas e a profundidade do objeto
A distribuição de temperaturas em materiais irradiados por laser é determinada pela potência, tamanho e forma do feixe de laser, juntamente com as propriedades do material que está sendo irradiado. A
Com base nas taxas de transferência de calor por condução adimensionais para os casos 12–15 na Tabela 4.1 b , encontre fatores de forma para os seguintes objetos com temperatura T 1 , localizados na s
Vapor d’água pressurizado a 450K escoa através de um tubo comprido de parede delgada com 0,5m de diâmetro. O tubo encontra-se no interior de um invólucro de concreto com seção transversal quadrada de
Um tubo com 50m m de diâmetro tem uma temperatura superficial de 85 ° C e está inserido no plano central de uma placa de concreto com 0,1m de espessura, cujas superfícies superior e inferior estão a 2