Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 02
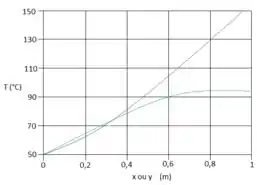
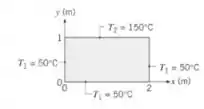
Uma placa retangular bidimensional está sujeita às condições de contorno especificadas. Usando os resultados da solução exata para a equação do calor apresentados na Seção 4.2, calcule a temperatura no ponto central , utilizando os cinco primeiros termos não nulos da série infinita que deve ser determinada. Avalie o erro decorrente do uso somente dos três primeiros termos da série infinita. Represente graficamente as distribuições de temperaturas e .
Passo 1
Fala aí! Olha só, essa questão quer primeiro que a gente encontre o valor da temperatura no ponto dado, e depois pede pra gente representar graficamente as distribuições de temperaturas, beleza?
Relaxa que a gente dá conta juntos!
Vamos nessa!
Passo 2
Como estamos trabalhando com uma série infinita, vamos utilizar a equação:
Como nosso enunciado diz que vamos fazer os cálculos no ponto central, isso quer dizer que estamos na metade exata de cada comprimento, ou seja:
Agora vamos substituir tudo isso na equação:
Estabelecendo a série infinita de 5 termos não nulos podemos considerar os cinco primeiros números ímpares positivos, beleza?
Ficamos então com , e colocando isso na nossa equação ficaremos com:
Passo 3
Estamos quase lá! Vamos agora achar a temperatura:
Precisamos então fazer a mesma coisa para os três primeiros termos da série, e verificar o erro da temperatura… Vamos nessa!
Opa! Temos então um erro muito baixo… menor que ! Show! Agora só falta fazer o gráfico e a gente termina essa!
Nossa curva azul corresponde ao e a verde ao nosso :
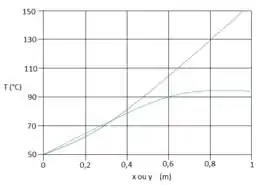
Resposta
Se usarmos apenas os três primeiros números da sequência temos um erro muito baixo, menor que .
