A água no sistema de irrigação de uma casa de campo deve ser retirada de um lago próximo. A casa está localizada em uma encosta 30 m acima da superfície do lago. A bomba está localizada em um terreno 3 m acima da superfície do lago. O dispositivo de irrigação (sprinkler) requer 40 L/min a 300 kPa. O sistema de tubos deve ser de ferro galvanizado com diâmetro de 2 cm. A seção de aspiração (entre o lago e a entrada da bomba) inclui uma entrada reentrante, um cotovelo padrão de 45°, um cotovelo padrão de 90° e 20 m de tubo. A seção de recalque (entre a saída da bomba e o sprinkler) inclui dois cotovelos-padrão de 45° e 45 m de tubo. Avalie a perda de carga no lado da sucção da bomba. Calcule a pressão manométrica na entrada da bomba. Determine o requisito de potência hidráulica da bomba. Se o diâmetro do tubo fosse aumentado para 4 cm, o requisito de potência da bomba decresceria, cresceria ou permaneceria o mesmo? Que diferença faria, se a bomba estivesse localizada no meio da encosta?

Vamos pegar alguns dados do fluido da Tabela A.7 do livro:

Agora com a velocidade encontrada no passo 1, conseguimos encontrar o número de Reynolds. Então, Reynolds será:

Agora, para encontrar o fator de atrito, precisamos primeiro pegar o dado referente à rugosidade da tubulação, que se encontra na tabela a seguir presente no capítulo 8:

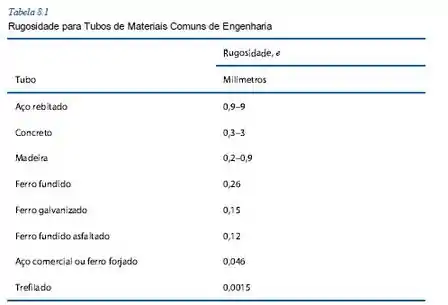
Então, como temos ferro galvanizado, então teremos . Então agora podemos usar a equação de Colebrook e descobrir o valor do fator de atrito:

Substituindo os valores conhecidos (lembrando que só conseguimos resolver essa equação com o auxílio de uma calculadora), temos:

Agora vamos voltar à equação do equilíbrio de energia do passo 1:

E substituir a expressão encontrada para a perda de carga no passo 1:

Agora precisamos recorrer às tabelas 8.2 e 8.4 apresentadas no livro e o diagrama para contração/expansão para encontrar os coeficientes de perda:

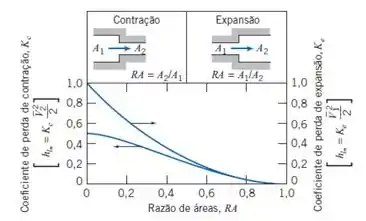
Nesse exercício, no trecho entre o lago e a bomba, temos dois cotovelos padrão, um de 90° e outro de 45°, então o comprimento equivalente será:

E o enunciado nos disse também que temos uma entrada reentrante, então:

Então a perda de carga no lado de sucção da bomba será:

Agora que temos todos os dados, podemos substituir os valores conhecidos na equação de energia do passo 4, então:

Agora, vamos repetir a análise, só que entre os pontos da saída da bomba (ponto 3) e o sprinkler (ponto 4), então, temos:

Substituindo o valor para a perda de carga:

Como a geometria da tubulação não muda, teremos e poderemos cancelar esses dois termos de velocidade. Nesse caso, teremos o comprimento . Como temos dois cotovelos padrão de 45°, então:

E, não temos nenhuma entrada ou saída brusca, então:

Dessa forma, substituindo os valores conhecidos na equação de energia, temos:

E, agora, conseguimos calcular a altura de carga da bomba:

E com isso, podemos encontrar a potência hidráulica para a bomba, dada por:

Substituindo os valores conhecidos:

Agora, refazendo os cálculos para , temos a nova velocidade:

Então, para esse caso, Reynolds será:

E o fator de atrito através de Colebrook:

Para a pressão em 2, substituindo os novos valores na mesma equação obtida no passo 4, teríamos:

Agora, calculando a pressão através da equação do passo 6, temos:

E, agora, conseguimos calcular a altura de carga da bomba:

E com isso, podemos encontrar a potência hidráulica para a bomba, dada por:

Substituindo os valores conhecidos:

A bomba não deve ser movida colina acima, se esse fosse o caso, ela necessitaria de mais potência para fornecer a mesma vazão ao escoamento. Caso queria mover a bomba, quanto mais próximo do lago, melhor, para aumentar a velocidade com que o fluido é transportado.