Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas Abrangentes - Ex. 9

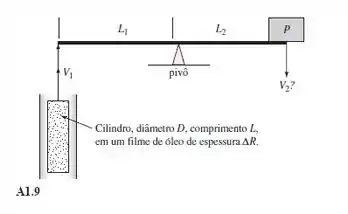
A alavanca da Figura A1.9 tem um peso P em uma das extremidades e está presa a um cilindro na outra extremidade. O cilindro tem peso e empuxo desprezíveis e desliza para cima em um filme de óleo pesado de viscosidade μ . (a) Se não houver aceleração (rotação uniforme da alavanca), deduza uma fórmula para a velocidade de queda V 2 do peso. Despreze o peso da alavanca. Considere um perfil de velocidade linear no filme de óleo. (b) Calcule a velocidade de queda do peso se P = 20   N ,   L 1 = 75   c m ,   L 2 = 50   c m ,   D = 10   c m ,   L = 22 c m ,   Δ R = 1   m m e o óleo é glicerina a 20 °C.

Passo 1

Bora boraaaa!

Com o movimento uniforme sem aceleração, os momentos se equilibram no pivô, assim:

∑ M p i v o = 0 = P L 2 - F 1 L 1

Temos que,

F 1 = τ A = μ V 1 Δ R ⋅ π D L

Como a alavanca é rígida, teremos que as velocidades do ponto final vão variar de acordo com seus comprimentos a partir do pivô, logo, tendo a rotação uniforme da alavanca:

V 1 = Ω L 1         e         V 2 = Ω L 2 → V 1 L 1 = V 2 L 2

Combinando as duas relações, e substituindo F 1 :

V 2 = P Δ R μ π D L L 2 L 1 2

Passo 2

Agora, em (B), vamos substituir os dados, tendo em vista que μ g l i c e r i n a = 1,49 k g m ⋅ s , assim:

V 2 = 20   N ⋅ 0,001   m 1,49 k g m ⋅ s π 0,1   m 0,22 m 75 c m 50 c m 2 ≈ 44   m / s

Resposta

  1. V 2 = P Δ R μ π D L L 2 L 1 2
  2. 44   m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura 1.8 , se o fluido é glicerina a 20° C e a distância entre as placas é 6m m , qual é a tensão de cisalhamento (em P a ) necessária para mover a placa superior a 5,5m / s ? Qual é o número de
Os dutos são limpos passando-se por dentro deles um cilindro de diâmetro justo chamado de p i g . O nomep i g (porco, em inglês) vem do ruído agudo que ele faz quando percorre o interior do duto. A Re
Um bloco de peso P desliza para baixo em um plano inclinado lubrificado por um filme fino de óleo, como mostra a Figura P 1.45 . A área de contato do filme é A e sua espessura é h . Considerando uma d
Conhecendo m para o ar a 20° C da Tabela 1.4 , calcule a sua viscosidade a 500° C (a) pela lei de potência e (b) pela lei de S u t h e r l a n d . Faça também uma estimativa com base na (c) Figura 1.7
Um modelo simples e popular para os dois fluidos não newtonianos da Figura 1.9a é a lei de potência: τ ≈ C d u d y n em que C e n são constantes ajustadas ao fluido [ 16 ] . Da Figura 1.9 a , deduza o