Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 46
Um modelo simples e popular para os dois fluidos não newtonianos da Figura 1.9a é a lei de potência:
em que e são constantes ajustadas ao fluido . Da Figura , deduza os valores do expoente para os quais o fluido é (a) newtoniano, (b) dilatante e (c) pseudoplástico. Considere a constante específica de modelo , com o fluido sofrendo cisalhamento entre duas placas paralelas como na Figura . Se a tensão de cisalhamento no fluido é , calcule a velocidade da placa superior para os casos (d, (e) e (f) .
Passo 1
E aí, tudo bem? Bora matar essa questão rapidinho!
Preciso que você me ajude um pouquinho nessa questão! Então vamos lá!
Na página do livro texto encontramos a figura , observando-a, vemos que:
Passo 2
(a)
Se , nossa equação tem um caráter linear, assim sendo considerado de acordo com a figura, um fluído newtoniano!
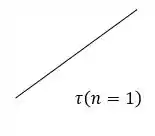
Passo 3
(b)
Se , nossa equação terá um acentuamento para cima, assim sendo considerado de acordo com a figura, um fluído dilatante!
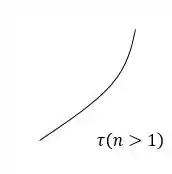
Passo 4
(c)
Se , nossa equação terá uma curvatura voltada para o eixo , assim sendo considerado de acordo com a figura, um fluído pseudoplástico!
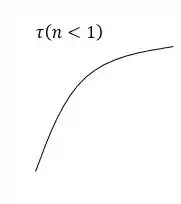
Passo 5
(d)
Estamos quase lá! Vamos utilizar a equação com os dados apresentados na questão:
A imagem se encontra no final da página !
Substituindo na formula, temos:
Isolando e resolvendo, temos que:
Passo 6
(e)
Só precisamos repetir para os demais casos, assim:
Isolando e resolvendo, temos que:
Passo 7
(f)
Pra matar de vez:
Isolando e resolvendo, temos que:
Isso é tudo pessoal, conseguimos mais uma! \o/
