Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 134

Uma aleta plana fabricada com a liga de alumínio 2024 k   =   185 W m K tem uma espessura na base de t   =   3   m m e um comprimento de 15 mm. Sua temperatura na base é T b = 100 ° C e ela está exposta a um fluido no qual T ∞ = 20 ° C e h   =   50 W m 2 K . Para as condições anteriores e uma aleta de largura unitária, compare a taxa de transferência de calor na aleta, a eficiência e o volume para os perfis retangular, triangular e parabólico.

Passo 1

Vamos seguir galerinhaaa !!

Preparados ??

Vamos dar uma olhada mais de perto nas expressões para cada uma delas:

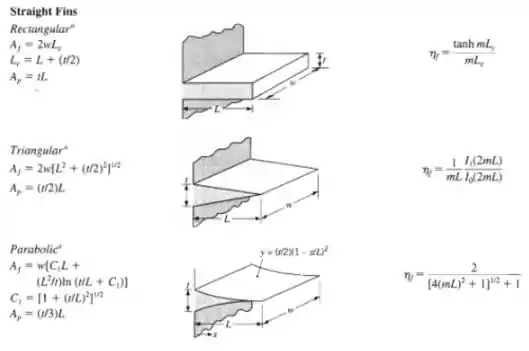
Nós precisamos achar três coisas aqui: taxa de transferência de calor na aleta, a eficiência e o volume !!

Vamos começar pela aleta retangular, ok? A eficiência pode ser calculada como:

η a = tanh ⁡ m L C m L C

Se:

L C = L + t 2

m = h P k A p = h 2 L + 2 t k t L

Como L ≫ t :

m = h 2 L k t L = 2 h k t

Sabendo que:

k   =   185 W m K

h   =   5 0 W m 2 K

t = 3   m m = 0,00 3   m

L = 15   m m = 0,015   m

T b = 100 ° C

T ∞ = 20 ° C

Então:

m = 2 5 0 W m 2 K   185 W m K 0,00 3   m = 13,4   m - 1

L C = 0,015   m + 0,003   m 2 = 0,0165   m

Na fórmula:

η a = tanh ⁡ ( 13,4   m - 1 × 0,0165   m ) ( 13,4   m - 1 × 0,0165   m ) = 0,982

O calor pode ser calculado em função da eficiência:

q ' a = η a h A f θ b

Como:

A f = 2 w L C

θ b = T b - T ∞

Considerando a largura unitária:

q ' a = 2 η a h L c T b - T ∞

Substituindo:

q ' a = 2 0,982 5 0 W m 2 K 0,0165   m 100 - 20 K

q ' a = 129,6 W m

E o volume é dado por:

V = A p = t L

Substituindo:

V = 0,003   m 0,015   m = 4,5 × 10 - 5 m 2

Passo 2

Para a aleta triangular, a eficiência pode ser calculada usando a fórmula dada ou o gráfico que vamos mostrar:

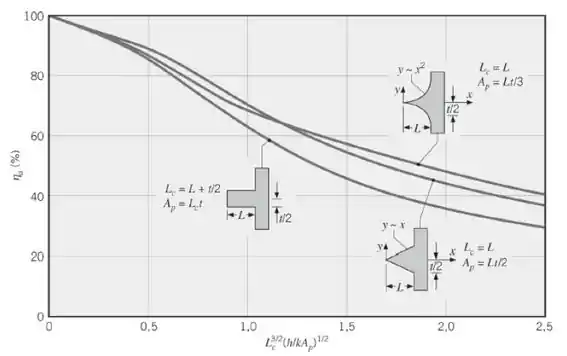
Eu vou usar o gráfico, certo?

L C 3 2 h k A p = L 3 2 2 h k L t

Substituindo:

L C 3 2 h k A p = 0,015   m 3 2 2 50 W m 2 K   185 W m K 0,003   m 0,015   m = 0,2

Olhando no gráfico:

η a = 0,9 78

O calor pode ser calculado em função da eficiência:

q ' a = η a h A f θ b

Como:

A f = 2 w L 2 + t 2 4 1 2 = 2 0,015   m 2 + 0,003   m 2 4 1 2 = 0,03   m 2

Então:

q ' a = 0,9 78 50 W m 2 K 0,03   m 2 100 - 20 K

q ' a = 117 , 3   W m

E o volume é dado por:

V = A p = t 2 L

Substituindo:

V = 0,003   m 2 0,015   m = 2,2 5 × 10 - 5 m 2

Passo 3

E o último perfil é a aleta parabólica, e eu vou optar novamente pelo gráfico, ok?

L C 3 2 h k A p = L 3 2 3 h k L t

Substituindo:

L C 3 2 h k A p = 0,015   m 3 2 3 50 W m 2 K   185 W m K 0,003   m 0,015   m = 0,2 5

Olhando no gráfico:

η a = 0,9 63

O calor pode ser calculado em função da eficiência:

q ' a = η a h A f θ b

Como:

A f = C 1 L + L 2 t ln ⁡ t L + C 1

Onde:

C 1 = 1 + t L 2 1 2

Então:

A f = 1 + t L 2 1 2 L + L 2 t ln ⁡ t L + 1 + t L 2 1 2

Substituindo:

A f = 1 + 0,003   m 0,015   m 2 1 2 0,015   m + 0,015   m 2 0,003   m ln ⁡ 0,003   m 0,015   m + 1 + 0,003   m 0,015   m 2 1 2

A f = 0,03   m 2

Colocando na fórmula do calor:

q ' a = 0,9 63 50 W m 2 K 0,03   m 2 100 - 20 K

q ' a = 11 5 , 6   W m

E o volume é dado por:

V = A p = t 3 L

Substituindo:

V = 0,003   m 3 0,015   m = 1 , 5 × 10 - 5 m 2

E assim nós fechamos mais uma com chave de ouro !!

Resposta

R e t a n g u l a r :     η a = 0,982             q ' a = 129,6 W m             V = 4,5 0 × 10 - 5 m 2 ;

T r i a n g u l a r :     η a = 0,9 7 8               q ' a = 117 , 3   W m           V = 2,25 × 10 - 5 m 2 ;

P a r a b ó l i c a :     η a = 0,9 63                 q ' a = 11 5 , 6   W m         V = 1 , 5 0 × 10 - 5 m 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bastão de latão com 100 mm de comprimento e 5 mm de diâmetro se estende horizontalmente a partir de uma peça a 200°C. O bastão encontra-se em um ambiente com T ∞ = 20 ° C eh=30 W m 2 K . Quais são
A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo. Considere um
A intensidade na qual a condição na extremidade afeta o desempenho térmico de uma aleta depende da geometria da aleta e de sua condutividade térmica, assim como do coeficiente convectivo. Considere um
Aletas planas triangulares e parabólicas estão submetidas às mesmas condições térmicas que a aleta plana retangular do Problema 3.134.Determine o comprimento de uma aleta triangular, de largura unitár
Dois longos bastões de cobre, com diâmetro D = 10 mm, serão soldados ponta a ponta com uma solda com ponto de fusão de 650°C. Os bastões encontram-se em um ambiente a 25°C com um coeficiente de transf