Um longo elemento aquecedor cilíndrico, com diâmetro D = 10 mm, temperatura T1 = 1500 K e emissividade ε1 = 1, é utilizado em um forno. A área da base do forno A2 é uma superfície cinza e difusa, com ε2 = 0,6 e é mantida a T2 = 500 K. As paredes lateral e superior são fabricadas com um tijolo refratário isolante, que é difuso e cinza, com ε = 0,9. O comprimento

do forno na direção normal à página é muito grande quando comparado com a largura w e a altura h.

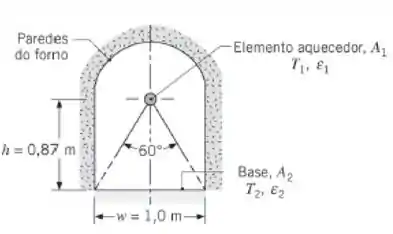
Desprezando a convecção e tratando as paredes do forno como isotérmicas, determine a potência por unidade de comprimento que deve ser suprida ao elemento aquecedor para manter condições de regime estacionário. Calcule a temperatura da parede do forno.

Precisamos conhecer , e , mas dessa vez as tabelas do livro não podem ajudar a gente!!

Só que olhando pra figura do livro a gente vê que a superfície tem contato com um ângulo de do cilindro, enquanto a superfície teria contato com , estrapolando a regra da soma podemos dizer que:

por sua vez:

E podemos aproximar !!

Lembrando que :

Calculando:

Agora só falta calcular a temperatura da parede do forno !!

Para isso vamos fazer um balanço da radiação, usando a equação do livro:

Sabendo que:

E é daí que a gente vai achar !!!

Substituindo os dados que temos:

Simplificando:

Para descobrir podemos usar a equação do livro:

Se solando e substituindo:

Podemos achar , lembrando que a superfície é um corpo negro:

E finalmente podemos calcular :

Calculando: