Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 69
Barras longas e cilíndricas são termicamente tratadas em um forno infravermelho. As barras, com diâmetro D = 50 mm, são colocadas sobre uma bandeja isolada e são aquecidas por um painel infravermelho acima delas, mantido a temperatura de Tp = 800 K, com εp = 0,85. As barras estão a Tb = 300 K e têm emissividade de εb = 0,92.
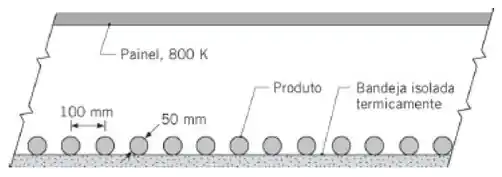
- Para um espaçamento do produto de s = 100 mm e um comprimento do produto de L = 1 m, determine o fluxo térmico radiante chegando ao produto. Determine o fluxo térmico na superfície do painel aquecedor.
- Represente graficamente o fluxo térmico radiante experimentado pelo produto e o fluxo térmico radiante no painel aquecedor na região 50 mm ≤ s ≤ 250 mm.
Passo 1
Vamos lá! O problema já trouxe pra a gente um esqueminha do que ta acontecendo e na letra , mas vamos só definir as superfícies :
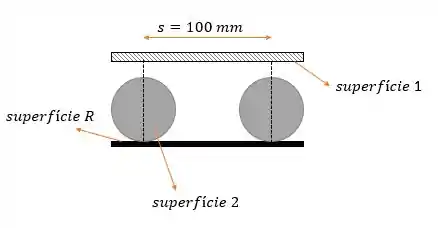
Queremos o fluxo térmico radiante e !!
Como temos uma superfície isolada, podemos usar a equação do livro pra achar a taxa termica radiante:
O fluxo térmico é:
Logo:
Sabendo que:
Pela regra da reciprocidade:
Substituindo todas as áreas:
Agora temos nossa equação prontinha, a gente só precisa achar as outras variáveis pra substituir!
Passo 2
Da tabela tiramos a expressão pro fator de forma :
Lembrando que:
Não precisa converter, afinal é adimensional:
A gente ainda precisa de e , pela regra da soma:
Logo:
Agora pela regra da simetria:
Passo 3
Sabendo que :
Calculando:
Passo 4
Agora só falta , lembrando que:
Mas:
Então:
Lembrando que:
Então:
Calculando:
Passo 5
Para a letra a gente quer representar graficamente a dependencia dos fluxos térmicos encontrados com !
Lembrando que:
Podemos isolar :
Então:
Logo:
Seguindo o mesmo raciocínio:
Ficamos com:
Passo 6
Então já temos as nossas equações:
Vamos variar :
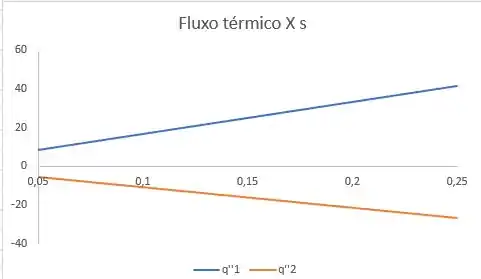
Plotando:
