Dois discos paralelos alinhados, com 0,4 m de diâmetro e separados por uma distância de 0,1 m, estão localizados em uma grande sala cujas paredes são mantidas a 300 K. Um dos discos é mantido a uma temperatura uniforme de 500 K, com uma emissividade de 0,6, enquanto o lado de trás do segundo disco encontra-se isolado termicamente. Se os discos são superfícies cinza e difusas, determine a temperatura do disco isolado.
Passo 1
Vamos lá!! Pegando tudo que o enunciado ta dizendo pra a gente e fazendo um esqueminha:
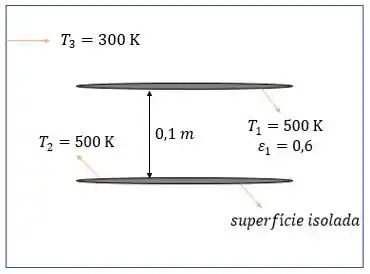
E queremos encontrar !! Vamos começar fazendo um balanço de energia na placa :
Como a superfície é isolada, então , e:
Opaaa, nossa temperatura apareceu:
Agora a gente vai atrás das outras informações pra poder acha !!
Passo 2
Como a sala tem uma área muito maior que dos discos, então vamos considerar a sala como um corpo negro, com isso:
Lembrando que :
Precisamos achar e , pela regra da soma:
Agora usando a regra da reciprocidade:
Como :
Temos dois discos paralelos coaxiais, para descobrir vamos recorrer a Figura , para isso precisamos de:
Temos que achar a curva , e achar no ponto onde a curva atravessa a linha vertical:
Achamos que é e !!!!
Podemos substituir todas as informações:
Podemos colocar em evidência e dar uma organizadinha no resto:
pode ir embora e simplificando :
Ok, agora precisamos conhecer !
Passo 3
Vamos fazer outro balanço de energia, agora da superfície :
Mas :
Vamos juntar isso e colocar em evidência:
pode ir embora e ficamos com:
Calculando :
Conhecemos , vamos usar a regra da soma:
Ficamos com:
Vamos substituir os dados que a gente tem:
Simplificando:
Passo 4
Bingo!! Temos duas equações duas icógnitas:
Substituindo em :
Calculamos:
Podemos achar :
Calculando:
Aweeeee!!!